题目内容
 如图,直线
如图,直线 交y轴于点A,交x轴于点B,点C为OA中点,则点C关于直线AB对称点C′的坐标是________.
交y轴于点A,交x轴于点B,点C为OA中点,则点C关于直线AB对称点C′的坐标是________.
(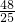 ,
, )
)
分析:先求出点A、B的坐标,再利用勾股定理列式求出AB的长,设CC′与AB相交于点P,利用相似三角形对应边成比例求出CP,根据对称性求出CC′,过点C′作C′D⊥y轴于D,再利用相似三角形对应边成比例列式求出CD、C′D,然后求出OD的长,写出点C′的坐标即可.
解答: 解:令x=0,则y=4,
解:令x=0,则y=4,
令y=0,则- x+4=0,
x+4=0,
解得x=3,
所以,点A(0,4),B(3,0),
∴OA=4,OB=3,
∵C为OA中点,
∴AC=OC= OA=
OA= ×4=2,
×4=2,
根据勾股定理,AB= =
= =5,
=5,
设CC′与AB相交于点P,
则△ACP∽△ABO,
∴ =
= ,
,
即 =
= ,
,
解得CP= ,
,
∴CC′=2CP=2× =
= ,
,
过点C′作C′D⊥y轴于D,
易得△C′CD∽△ABO,
∴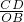 =
= =
= ,
,
即 =
= =
= ,
,
解得CD=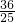 ,C′D=
,C′D=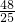 ,
,
∴OD=OC+CD=2+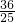 =
= ,
,
∴点C′的坐标为(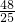 ,
, ).
).
故答案为:(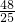 ,
, ).
).
点评:本题考查了一次函数图象上点的坐标特征,坐标与图形变化-对称,主要利用了相似三角形的判定与性质,作辅助线构造出相似三角形是解题的关键.
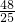 ,
, )
)分析:先求出点A、B的坐标,再利用勾股定理列式求出AB的长,设CC′与AB相交于点P,利用相似三角形对应边成比例求出CP,根据对称性求出CC′,过点C′作C′D⊥y轴于D,再利用相似三角形对应边成比例列式求出CD、C′D,然后求出OD的长,写出点C′的坐标即可.
解答:
 解:令x=0,则y=4,
解:令x=0,则y=4,令y=0,则-
 x+4=0,
x+4=0,解得x=3,
所以,点A(0,4),B(3,0),
∴OA=4,OB=3,
∵C为OA中点,
∴AC=OC=
 OA=
OA= ×4=2,
×4=2,根据勾股定理,AB=
 =
= =5,
=5,设CC′与AB相交于点P,
则△ACP∽△ABO,
∴
 =
= ,
,即
 =
= ,
,解得CP=
 ,
,∴CC′=2CP=2×
 =
= ,
,过点C′作C′D⊥y轴于D,
易得△C′CD∽△ABO,
∴
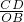 =
= =
= ,
,即
 =
= =
= ,
,解得CD=
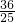 ,C′D=
,C′D=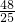 ,
,∴OD=OC+CD=2+
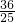 =
= ,
,∴点C′的坐标为(
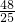 ,
, ).
).故答案为:(
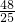 ,
, ).
).点评:本题考查了一次函数图象上点的坐标特征,坐标与图形变化-对称,主要利用了相似三角形的判定与性质,作辅助线构造出相似三角形是解题的关键.

练习册系列答案
相关题目
 已知:抛物线
已知:抛物线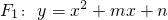 的顶点为A(1,0)
的顶点为A(1,0)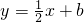 交x轴于点C,交y轴于点D,在抛物线F1上有一点B,且点B与点A关于直线
交x轴于点C,交y轴于点D,在抛物线F1上有一点B,且点B与点A关于直线 ?若存在试求n的值;若不存在,请说明理由.
?若存在试求n的值;若不存在,请说明理由. 如图,直线
如图,直线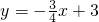 交x轴于点A,交y轴于点B,第一象限内的点P(a,b)是经过点B的直线n上的一点,过点P作PD⊥y轴于点D,连结PA.
交x轴于点A,交y轴于点B,第一象限内的点P(a,b)是经过点B的直线n上的一点,过点P作PD⊥y轴于点D,连结PA. 交x轴于点A,交直线
交x轴于点A,交直线 于点B(2,m).矩形CDEF的边DC在x轴上,D在C的左侧,EF在x轴的上方,DC=2,DE=4.当点C的坐标为(-2,0)时,矩形CDEF开始以每秒2个单位的速度沿x轴向右运动,运动时间为t秒.
于点B(2,m).矩形CDEF的边DC在x轴上,D在C的左侧,EF在x轴的上方,DC=2,DE=4.当点C的坐标为(-2,0)时,矩形CDEF开始以每秒2个单位的速度沿x轴向右运动,运动时间为t秒.
 交x轴于点A,交直线
交x轴于点A,交直线 于点B(2,m).矩形CDEF的边DC在x轴上,D在C的左侧,EF在x轴的上方,DC=2,DE=4.当点C的坐标为(-2,0)时,矩形CDEF开始以每秒2个单位的速度沿x轴向右运动,运动时间为t秒.
于点B(2,m).矩形CDEF的边DC在x轴上,D在C的左侧,EF在x轴的上方,DC=2,DE=4.当点C的坐标为(-2,0)时,矩形CDEF开始以每秒2个单位的速度沿x轴向右运动,运动时间为t秒.
 交x轴于点B,交y轴于点C,点A为x轴正半轴上一点,AO=CO,△ABC的面积为12.
交x轴于点B,交y轴于点C,点A为x轴正半轴上一点,AO=CO,△ABC的面积为12.