题目内容
20．若关于x的方程（m-1）x2-3x-2=0有两个实数根，则m的取值范围是m≥-$\frac{17}{8}$且m≠1．分析 根据已知得出不等式m-1≠0，△=（-3）2-4（m-1）•（-2）≥0，求出即可．
解答 解：∵关于x的方程（m-1）x2-3x-2=0有两个实数根，
∴m-1≠0，△=（-3）2-4（m-1）•（-2）≥0，
解得：m≥-$\frac{17}{8}$且m≠1，
故答案为：m≥-$\frac{17}{8}$且m≠1．
点评 本题考查了根的判别式的应用，能熟记根的判别式的内容是解此题的关键．
练习册系列答案
名校课堂系列答案
相关题目
有理数a、b、c在数轴上的位置如图，|a|-|a+b|-|c-a|+|b-c|=-a．
如图，在△ABC外作两个大小不同的等腰直角三角形，其中∠DAB=∠CAE=90°，AB=AD，AC=AE，连结DC、BE交于F点．
15．二次函数y=-（x+1）2-2的顶点坐标是（ ）
| A． | （1．-2） | B． | （-1．-2 ） | C． | （1.2） | D． | （-1.2） |
有一个面积为30平方米的长方形ABCD的鸡场，鸡场的一边靠墙（墙长8米），墙的对面有一个1米宽的门，另三边用竹篱笆围成，篱笆总长15米，求鸡场的宽AB是多少米？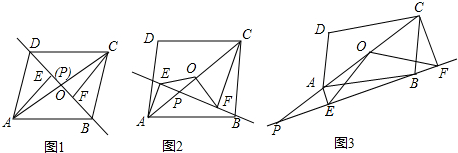
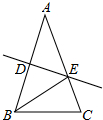如图，在△ABC中，边AB的垂直平分线交AC于E，△ABC与△BEC的周长分别为24
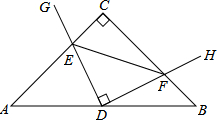在Rt△ABC中，AC=BC，点D为AB中点．∠GDH=90°，∠GDH绕点D旋转，DG、DH分别与边AC、BC交于E，F两点．下列结论：