题目内容
关于x的方程(k-2)x2-2(k-1)x+k+1=0有实数根,求k的取值范围.
考点:根的判别式,一元二次方程的定义
专题:
分析:分两种情况:①k-2≠0时,由△=[-2(k-1)]2-4(k-2)(k+1)≥0,解不等式即可;②当k-2=0时为一元一次方程,方程有一根.
解答:解:分两种情况:
①k-2≠0时,
∵关于x的方程(k-2)x2-2(k-1)x+k+1=0有实数根,
∴△=[-2(k-1)]2-4(k-2)(k+1)≥0,
解得k≤3,
∵k-2≠0,k≠2;
∴k的取值范围为k≤3且k≠2;
②当k-2=0时为一元一次方程,方程有一根.
综上所知k的取值范围为k≤3.
①k-2≠0时,
∵关于x的方程(k-2)x2-2(k-1)x+k+1=0有实数根,
∴△=[-2(k-1)]2-4(k-2)(k+1)≥0,
解得k≤3,
∵k-2≠0,k≠2;
∴k的取值范围为k≤3且k≠2;
②当k-2=0时为一元一次方程,方程有一根.
综上所知k的取值范围为k≤3.
点评:本题主要考查了根的判别式,总结:一元二次方程根的情况与判别式△的关系:
(1)△>0?方程有两个不相等的实数根;
(2)△=0?方程有两个相等的实数根;
(3)△<0?方程没有实数根.
进行分类讨论是解题的关键.
(1)△>0?方程有两个不相等的实数根;
(2)△=0?方程有两个相等的实数根;
(3)△<0?方程没有实数根.
进行分类讨论是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,在平面直角坐标系中,反比例函数y1=
如图,在平面直角坐标系中,反比例函数y1=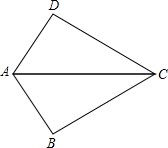 如图,已知AB=AD,那么添加下列一个条件后,能用SAS判定△ABC≌△ADC的是
如图,已知AB=AD,那么添加下列一个条件后,能用SAS判定△ABC≌△ADC的是