题目内容
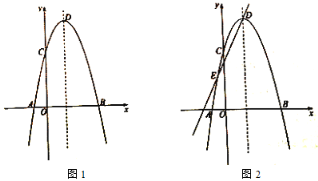
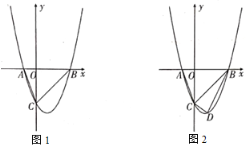
【题目】如图1,在平面直角坐标系中,二次函数![]() 交
交![]() 轴于
轴于![]() 、
、![]() 两点,(点
两点,(点![]() 在点
在点![]() 的左侧)与
的左侧)与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() .
.
(1)求点![]() 、点
、点![]() 和点
和点![]() 的坐标;
的坐标;
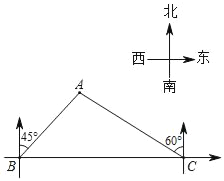
(2)如图2,若点![]() 为第四象限内抛物线上一动点,点
为第四象限内抛物线上一动点,点![]() 的横坐标为
的横坐标为![]() ,
,![]() 的面积为
的面积为![]() .求
.求![]() 关于
关于![]() 的函数关系式,并求出
的函数关系式,并求出![]() 的最大值;
的最大值;
(3)抛物线的对称轴上是否存在点![]() ,使
,使![]() 为等腰三角形?若存在,请直接写出所有点
为等腰三角形?若存在,请直接写出所有点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
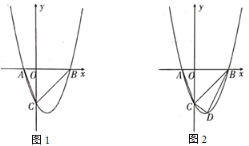
【答案】(1)![]() ,
,![]() ,
,![]() ;(2)
;(2)![]() ;
;![]() ;(3)
;(3)![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
【解析】
(1))求当![]() 时和当
时和当![]() 时的解即可(2)根据
时的解即可(2)根据![]() 点的位置结合二次函数的图象和性质求
点的位置结合二次函数的图象和性质求![]() 和
和![]() ,从而求得面积的最大值(3)先求出函数的对称轴,设点
,从而求得面积的最大值(3)先求出函数的对称轴,设点![]() 的坐标,再根据等腰三角形性质分情况讨论求解.
的坐标,再根据等腰三角形性质分情况讨论求解.
(1)当![]() 时,
时,![]() ,解得
,解得![]() ,
,![]() ,
,
又∵![]() 在
在![]() 的左侧,
的左侧,
∴![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,∴
,∴![]() .
.
(2)∵![]() 的横坐标为
的横坐标为![]() ,
,![]() 在抛物线上.
在抛物线上.
∴![]() 的纵坐标为
的纵坐标为![]() ,∴
,∴![]() ,
,
∵点![]() 在第四象限,∴
在第四象限,∴![]() ,
,![]() ,
,
连接![]() ,
,
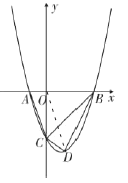
∵![]() ,
,
![]() ,
,
![]() .
.
∴![]()
![]()
![]()
![]() .
.
∵![]() ,∴当
,∴当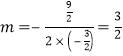 时,
时,
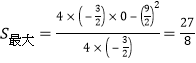 .
.
(3)二次函数![]() 的对称轴是
的对称轴是![]()
设点P的坐标为![]() ,又因为
,又因为![]()
![]()
![]()
![]()
分三种情况讨论:
当![]() 时,
时,![]()
解得![]() ,此时
,此时![]() ,
,
当![]() 时,
时,![]()
解得![]() ,此时
,此时![]() ,
,![]() ,
,
当![]() 时,
时,![]()
解得![]() ,此时
,此时![]() ,
,![]()
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目