题目内容
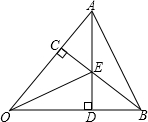如图，在△ABO中，AD⊥OB于D，BC⊥OA于C，AD，BC交于点E，且OE平∠AOB，求证：△AEB是等腰三角形．
证明：∵AD⊥OB于D，BC⊥OA于C，AD，BC交于点E，且OE平∠AOB，
∴∠ACE=∠BDE=90°，CE=DE，
在△ACE和△BDE中，
∠ACE=∠BDE，CE=DE，∠AEC=∠BED，
∴△ACE≌△BDE，
∴AE=BE，
∴△AEB是等腰三角形．
分析：根据角平分线性质推出DE=CE，证△ACE≌△BDE，推出AE=BE即可．
点评：本题考查了角平分线性质、等腰三角形的判定和性质、全等三角形的判定和性质，关键是通过全等三角形推出AE=BE．
∴∠ACE=∠BDE=90°，CE=DE，
在△ACE和△BDE中，
∠ACE=∠BDE，CE=DE，∠AEC=∠BED，
∴△ACE≌△BDE，
∴AE=BE，
∴△AEB是等腰三角形．
分析：根据角平分线性质推出DE=CE，证△ACE≌△BDE，推出AE=BE即可．
点评：本题考查了角平分线性质、等腰三角形的判定和性质、全等三角形的判定和性质，关键是通过全等三角形推出AE=BE．
练习册系列答案
全优冲刺100分系列答案
英才点津系列答案
相关题目
是直线l，直线AC∥x轴交直线l与点C．
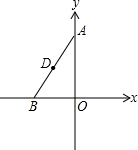如图，在△ABO中，已知A（0，4），B（-2，0），D为线段AB的中点．
（2013•崇左）如图，在△ABO中，OA=OB，C是边AB的中点，以O为圆心的圆过点C，且与OA交于点E，与OB交于点F，连接CE，CF．
如图，在△ABO中，AD⊥OB于D，BC⊥OA于C，AD，BC交于点E，且OE平∠AOB，求证：△AEB是等腰三角形．