题目内容
将一张长80cm、宽40cm的矩形铁皮卷成一个高为40cm的圆柱形水桶的侧面(接口损耗不计),则桶底的面积为
- A.
 cm2
cm2 - B.1600πcm2
- C.
 cm2
cm2 - D.6400πcm2
A
分析:桶底的面积=π半径2=π(矩形长÷2π)2.
解答:要求桶底的面积,先要求桶底的半径,已知桶底的周长是80cm,所以半径= cm.
cm.
∴桶底的面积= ×2=
×2= cm2,故选A.
cm2,故选A.
点评:本题的关键是理解如何把一个矩形卷成一个圆柱,矩形的长和宽分别充当了圆柱的什么,然后利用公式求值即可.
分析:桶底的面积=π半径2=π(矩形长÷2π)2.
解答:要求桶底的面积,先要求桶底的半径,已知桶底的周长是80cm,所以半径=
 cm.
cm.∴桶底的面积=
 ×2=
×2= cm2,故选A.
cm2,故选A.点评:本题的关键是理解如何把一个矩形卷成一个圆柱,矩形的长和宽分别充当了圆柱的什么,然后利用公式求值即可.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
将一张长80cm、宽40cm的矩形铁皮卷成一个高为40cm的圆柱形水桶的侧面(接口损耗不计),则桶底的面积为( )
A、
| ||
| B、1600πcm2 | ||
C、
| ||
| D、6400πcm2 |
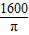 cm2
cm2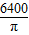 cm2
cm2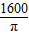 cm2
cm2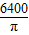 cm2
cm2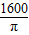 cm2
cm2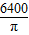 cm2
cm2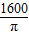 cm2
cm2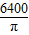 cm2
cm2