题目内容
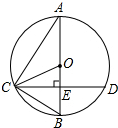 如图,已知AB为⊙O的直径,CD是弦,且AB⊥CD于点E.连接AC、OC、BC.
如图,已知AB为⊙O的直径,CD是弦,且AB⊥CD于点E.连接AC、OC、BC.(1)若∠A=30°,BC=2,求S扇形BOC.(结果保留π)
(2)若EB=8cm,CD=24cm,求⊙O的直径.
考点:垂径定理,勾股定理,扇形面积的计算
专题:
分析:(1)由AB为⊙O的直径,∠A=30°,BC=2,易求得直径AB的长,圆心角∠BOC的度数,继而求得S扇形BOC.
(2)首先设半径为xcm,由垂径定理,求得CE的长,然后由勾股定理,得方程:122+(x-8)2=x2,解此方程即可求得答案.
(2)首先设半径为xcm,由垂径定理,求得CE的长,然后由勾股定理,得方程:122+(x-8)2=x2,解此方程即可求得答案.
解答:解:(1)∵AB为⊙O的直径,
∴∠ACB=90°,
∵∠A=30°,BC=2,
∴AB=2BC=4,∠BOC=60°,
∴OE=2,
∴S扇形BOC=
=
π;
(2)∵AB为⊙O的直径,AB⊥CD,
∴CE=
CD=
×24=12(cm),
设⊙O的半径为xcm,则OE=x-8(cm),
在Rt△OCE中,CE2+OE2=OC2,
∴122+(x-8)2=x2,
解得:x=13,
∴⊙O的直径为26cm.
∴∠ACB=90°,
∵∠A=30°,BC=2,
∴AB=2BC=4,∠BOC=60°,
∴OE=2,
∴S扇形BOC=
| 60×π×22 |
| 360 |
| 2 |
| 3 |
(2)∵AB为⊙O的直径,AB⊥CD,
∴CE=
| 1 |
| 2 |
| 1 |
| 2 |
设⊙O的半径为xcm,则OE=x-8(cm),
在Rt△OCE中,CE2+OE2=OC2,
∴122+(x-8)2=x2,
解得:x=13,
∴⊙O的直径为26cm.
点评:此题考查了圆周角定理、垂径定理以及勾股定理.此题难度不大,注意掌握方程思想与数形结合思想的应用.

练习册系列答案
相关题目
长江比黄河长836千米,黄河长度的6倍比长江长度的5倍多1284千米,小东这段文字,设长江长为x千米,黄河长为y千米,然后通过列、解二元一次方程组,正确的求出了长江和黄河的长度,那么小东列的方程组可能是( )
A、
| |||||
B、
| |||||
C、
| |||||
D、
|
 如图,已知圆锥侧面展开图的扇形面积为65π cm2,扇形的弧长为10π cm,则圆锥母线长是( )
如图,已知圆锥侧面展开图的扇形面积为65π cm2,扇形的弧长为10π cm,则圆锥母线长是( )| A、5cm | B、10cm |
| C、12cm | D、13cm |
 如图,EB、EC是⊙O的两条切线,B、C为切点,A、D是⊙O上两点,∠E=46°,∠DCF=33°.求∠A的度数( )
如图,EB、EC是⊙O的两条切线,B、C为切点,A、D是⊙O上两点,∠E=46°,∠DCF=33°.求∠A的度数( )| A、90° | B、100° |
| C、110° | D、67° |
 将一张正方形纸片剪成四个大小、形状一样的小正方形(如图所示),记为第一次操作,然后将其中的一片又按同样的方法剪成四小片,记为第二次操作,如此循环进行下去.请将下表中空缺的数据填写完整,并解答所提出的问题:
将一张正方形纸片剪成四个大小、形状一样的小正方形(如图所示),记为第一次操作,然后将其中的一片又按同样的方法剪成四小片,记为第二次操作,如此循环进行下去.请将下表中空缺的数据填写完整,并解答所提出的问题: 如图,在平面直角坐标系中,三角形的顶点都在格点上,△BDE是由△ABC绕着某点逆时针旋转一定的角度得到的,则该点的坐标为
如图,在平面直角坐标系中,三角形的顶点都在格点上,△BDE是由△ABC绕着某点逆时针旋转一定的角度得到的,则该点的坐标为