题目内容
如图，在一棵树CD的10m高处的B点有两只猴子，它们都要到A处池塘边喝水，其中一只猴子沿树爬下走到离树20m处的池塘A处，另一只猴子爬到树顶D后直线跃入池塘的A处．如果两只猴子所经过的路程相等，试问这棵树多高？
分析：要求树的高度，就要求BD的高度，在直角三角形ACD中运用勾股定理可以列出方程式，CD2+AC2=AD2，其中CD=CB+BD．
解答：解：设BD高为x，则从B点爬到D点再直线沿DA到A点，走的总路程为x+AD，其中AD=
而从B点到A点经过路程（20+10）m=30m，
根据路程相同列出方程x+
=30，
可得
=30-x，
两边平方得：（10+x）2+400=（30-x）2，
整理得：80x=400，
解得：x=5，
所以这棵树的高度为10+5=15m．
故答案为：15m．
| (10+x)2+202 |
而从B点到A点经过路程（20+10）m=30m，
根据路程相同列出方程x+
| (10+x)2+202 |
可得
| (10+x)2+202 |
两边平方得：（10+x）2+400=（30-x）2，
整理得：80x=400，
解得：x=5，
所以这棵树的高度为10+5=15m．
故答案为：15m．
点评：本题考查的是勾股定理的灵活运用，要求在变通中熟练掌握勾股定理．
练习册系列答案
活力课时同步练习册系列答案
相关题目
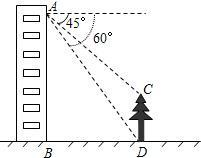如图，小芸在自家楼房的窗户A处，测量楼前的一棵树CD的高．现测得树顶C处的俯角为45°，树底D处的俯角为60°，楼底到大树的距离BD为20米．请你帮助小芸计算树的高度（精确到0.1米）．
如图，身高为1.6m的小李AB站在河的一岸，利用树的倒影去测对岸一棵树CD的高度，CD的倒影是C′D，且AEC′在一条视线上，河宽BD=12m，且BE=2m，则树高CD=
121、如图，有两只猴子在一棵树CD高5m的点B处，它们都要到A处的池塘去喝水，其中一只猴子沿树爬下走到离树10m处的池塘A处，另一只猴子爬到树顶D后直线越向池塘的A处．如果两只猴子所经过的路程相等，这棵树高有多少米？