题目内容
1．一个容器盛满纯药液63L，第一次倒出一部分纯药液后，用水加满；第二次又倒出同样多的纯药液，此时，容器内剩下的纯药液是28L，则每次倒出的液体是多少？分析 设倒出药液为x升，第一次剩下的纯药液为63（1-$\frac{x}{63}$），第二次加满水再倒出x升溶液，剩下的纯药液为63（1-$\frac{x}{63}$）（1-$\frac{x}{63}$），又知道剩下的纯药液为28升，列方程即可求出x．
解答 解：设每次倒出药液x升，第一次倒出后剩（63-x）升药液，第二次倒出后还剩63-x-$\frac{63-x}{63}$×x=63$（1-\frac{x}{63}）^{2}$升药液，
即列方程为：63$（1-\frac{x}{63}）^{2}$=28．
解得x=21或x=105（不合题意，舍去）．即每次倒出21升．
点评 解题关键是要读懂题目的意思，根据题目给出的条件，找出合适的等量关系本题是个浓度问题，可把药液看成溶质，设出未知数求解．
练习册系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
已知不等式组$\left\{\begin{array}{l}{2x+3＞3x}\\{2x-（x-1）≥-3}\end{array}\right.$，
如图，把两个大小相同的含30°的角的三角尺如图放置，若AD=4$\sqrt{6}$，试求围成的△ADC的面积．
9．
如图中字母A所代表的正方形的面积为（ ）
如图中字母A所代表的正方形的面积为（ ）| A． | 12 | B． | 5 | C． | 10 | D． | 25 |
6．已知-3xm-1y3与$\frac{5}{2}$xym+n是同类项，那么m，n的值分别是（ ）
| A． | m=2，n=-1 | B． | m=-2，n=-1 | C． | m=-2，n=1 | D． | m=2，n=1 |
10．
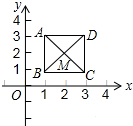如图，已知正方形ABCD，对角线的交点M（2，2）．规定“把正方形ABCD先沿x轴翻折，再向左平移1个单位”为一次变换．如此这样，连续经过2014次变换后，正方形ABCD的对角线交点M的坐标变为（ ）
如图，已知正方形ABCD，对角线的交点M（2，2）．规定“把正方形ABCD先沿x轴翻折，再向左平移1个单位”为一次变换．如此这样，连续经过2014次变换后，正方形ABCD的对角线交点M的坐标变为（ ）| A． | （-2012，2） | B． | （-2012，-2） | C． | （-2013，-2） | D． | （-2013，2） |
已知a，b，c为有理数，且它们在数轴上的位置如图所示．