题目内容
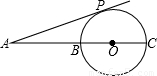
 如图,BC是⊙O直径,P是CB延长线上一点,PA切⊙O于A,若∠P=30°,PA=
如图,BC是⊙O直径,P是CB延长线上一点,PA切⊙O于A,若∠P=30°,PA= ,则⊙O半径为________.
,则⊙O半径为________.
1
分析:连结OA,根据切线的性质得到OA⊥AP,则∠OAP=90°,在Rt△OPA中根据含30度的直角三角形三边的关系求OA即可.
解答: 解:连结OA,如图,
解:连结OA,如图,
∵PA切⊙O于A,
∴OA⊥AP,
∴∠OAP=90°,
在Rt△OPA中,∠P=30°,PA= ,
,
∴OA= AP=
AP= ×
× =1.
=1.
故答案为1.
点评:本题考查了切线的性质:圆的切线垂直于经过切点的半径;经过圆心且垂直于切线的直线必经过切点;经过切点且垂直于切线的直线必经过圆心.也考查了含30度的直角三角形三边的关系.
分析:连结OA,根据切线的性质得到OA⊥AP,则∠OAP=90°,在Rt△OPA中根据含30度的直角三角形三边的关系求OA即可.
解答:
 解:连结OA,如图,
解:连结OA,如图,∵PA切⊙O于A,
∴OA⊥AP,
∴∠OAP=90°,
在Rt△OPA中,∠P=30°,PA=
 ,
,∴OA=
 AP=
AP= ×
× =1.
=1.故答案为1.
点评:本题考查了切线的性质:圆的切线垂直于经过切点的半径;经过圆心且垂直于切线的直线必经过切点;经过切点且垂直于切线的直线必经过圆心.也考查了含30度的直角三角形三边的关系.

练习册系列答案
相关题目
 如图,BC是⊙O直径,点A为CB延长线上一点,AP切⊙O于点P,若AP=12,AB:BC=4:5,则⊙O的半径等于( )
如图,BC是⊙O直径,点A为CB延长线上一点,AP切⊙O于点P,若AP=12,AB:BC=4:5,则⊙O的半径等于( ) 如图,BC是⊙O直径,P是CB延长线上一点,PA切⊙O于A,若∠P=30°,PA=
如图,BC是⊙O直径,P是CB延长线上一点,PA切⊙O于A,若∠P=30°,PA= 如图,BC是直径,AD=DC,∠ADB=20°,∠ACB=
如图,BC是直径,AD=DC,∠ADB=20°,∠ACB=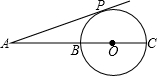 如图,BC是⊙O直径,点A为CB延长线上一点,AP切⊙O于点P,若AP=12,AB:BC=4:5,则⊙O的半径等于
如图,BC是⊙O直径,点A为CB延长线上一点,AP切⊙O于点P,若AP=12,AB:BC=4:5,则⊙O的半径等于