题目内容
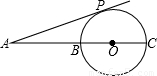
 如图,BC是直径,AD=DC,∠ADB=20°,∠ACB=
如图,BC是直径,AD=DC,∠ADB=20°,∠ACB=20°
20°
,∠DBC=35°
35°
.分析:根据圆周角定理首先得出∠ADB=∠ACB,即可得出∠ACB=20°,再利用圆心角定理以及直径所对的圆周角等于90°,即可得出∠DBC=∠DCA的度数.
解答:解:∵
=
,
∴∠ADB=∠ACB(同弧所对圆周角相等),
∵∠ADB=20°,
∴∠ACB=20°,
∵BC是直径,
∴∠BDC=90°(直径所对圆周角等于90°),
∵AD=DC,
∴
=
,
∴∠DBC=∠DCA(等弧所对圆周角相等),
∵∠ACB=20°,
∵∠BDC=∠DBC+∠DCB=90°,
∴∠DBC+∠DCA=∠DBC+∠DCB-∠ACB=90°-20°=70°,
∴∠DBC=∠DCA=35°.
故答案为:20°,35°.
 |
| AB |
 |
| AB |
∴∠ADB=∠ACB(同弧所对圆周角相等),
∵∠ADB=20°,
∴∠ACB=20°,
∵BC是直径,
∴∠BDC=90°(直径所对圆周角等于90°),
∵AD=DC,
∴
 |
| AD |
 |
| CD |
∴∠DBC=∠DCA(等弧所对圆周角相等),
∵∠ACB=20°,
∵∠BDC=∠DBC+∠DCB=90°,
∴∠DBC+∠DCA=∠DBC+∠DCB-∠ACB=90°-20°=70°,
∴∠DBC=∠DCA=35°.
故答案为:20°,35°.
点评:此题主要考查了圆周角定理以及其推论,根据圆周角定理得出∠BDC=90°以及∠DBC=∠DCA是解题关键.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
 如图,BC是⊙O直径,点A为CB延长线上一点,AP切⊙O于点P,若AP=12,AB:BC=4:5,则⊙O的半径等于( )
如图,BC是⊙O直径,点A为CB延长线上一点,AP切⊙O于点P,若AP=12,AB:BC=4:5,则⊙O的半径等于( ) 如图,BC是⊙O直径,P是CB延长线上一点,PA切⊙O于A,若∠P=30°,PA=
如图,BC是⊙O直径,P是CB延长线上一点,PA切⊙O于A,若∠P=30°,PA=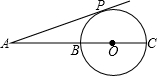 如图,BC是⊙O直径,点A为CB延长线上一点,AP切⊙O于点P,若AP=12,AB:BC=4:5,则⊙O的半径等于
如图,BC是⊙O直径,点A为CB延长线上一点,AP切⊙O于点P,若AP=12,AB:BC=4:5,则⊙O的半径等于