题目内容
【题目】点A为双曲线y=
（k≠0）上一点，B为x轴上一点，且△AOB为等边三角形，△AOB的边长为2，则k的值为（ ）
A. 2
B. ±2
C. 
D. ±
【答案】D
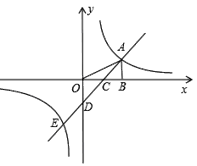
【解析】当k＞0时，设点A在第一象限，过A作AC⊥OB于C，
如图①，
∵OB＝2，
∴B点的坐标是(2，0)．
∵△AOB为等边三角形，∠AOC＝60°，AO＝2，
∴OC＝1， 
，
∴A点的坐标是(1， 
)．
∵点A为双曲线
(k≠0)上的一点，
∴
．
当k＜0时，设点A在第二象限，过A作AC⊥OB于C，如图②．
∵OB＝2．
∴B点的坐标是(－2，0)．
∵△AOB为等边三角形，∠AOC＝60°，AO＝2，
∴OC＝1， 
，
∴A点的坐标是(－1， 
)．
∵点A为双曲线
(k≠0)上的一点，
∴
．
综上， 
．
故选D．
练习册系列答案
相关题目
