题目内容

直线l：y=（m-3）x+n-2（m，n为常数）的图象如图，化简：|m-3|-
n2-4n+4
得（　　）精英家教网
A、3-m-nB、5
C、-1D、m+n-5
分析：先从一次函数的图象判断m-3的正负值，n-2的正负值，然后再化简原代数式．
解答：精英家教网解：直线l：y=（m-3）x+n-2（m，n为常数）的图象可知，
n-2＜0，m-3＞0．
|m-3|-
n2-4n+4

=m-3-
(n-2)2

=m-3+n-2
=m+n-5
故选D．
点评：本题主要考查二次函数的性质及其化简，绝对值的化简．
练习册系列答案
相关题目
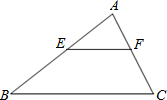精英家教网如图，在△ABC中，AE=EB，AF=FC，有一同学发现EF与BC存在以下关系：EF∥BC，且EF=
12
BC．
（1）请你用学过的知识来说明上述关系成立的理由．
（2）如图：在（1）的结论下，过BC、EF作直线，过A作BC的平行线．将AC向左平移到DC，得到图②，将AC向右平移到DC，得到图③．在图②和图③中猜想线段EF与线段AD、BC的关系，请把你猜想的结论填在图下的方框内，并说明理由．
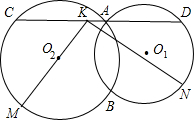精英家教网
精英家教网
精英家教网如图，⊙O1与⊙O2相交于点A和B，经过A作直线与⊙O1相交于D，与⊙O2相交于C，设弧BC的中点为M，弧BD的中点为N，线段CD的中点为K．求证：MK⊥KN．
如图1，抛物线y=ax2+bx（a＞0）与双曲线y=
kx
相交于点A，B．已知点A的坐标为（1，4），点B在第三象限内，且△AOB的面积为3（O为坐标原点）．
（1）求实数a，b，k的值；
（2）如图2，过抛物线上点A作直线AC∥x轴，交抛物线于另一点C，求所有满足△COE∽△BOA的点E的坐标（提示：C点的对应点为B）．
精英家教网精英家教网
如图，在平面直角坐标系中，直线AB与Y轴和X轴分别交于点A、点B，与反比例精英家教网函数y=
mx
在第一象限的图象交于点c（1，6）、点D（3，n）．过点C作CE上y轴于E，过点D作DF上x轴于F．
（1）求m，n的值；
（2）求直线AB的函数解析式；
（3）求证：△AEC≌△DFB．
25、已知：如图，DG⊥BC，AC⊥BC，EF⊥AB，∠1=∠2，求证：CD⊥AB．
证明：∵DG⊥BC，AC⊥BC（已知）
∴∠DGB=∠ACB=90°（垂直定义）
∴DG∥AC（
同位角相等，两直线平行
）
∴∠2=
∠ACD
（
两直线平行，内错角相等
）
∵∠1=∠2（已知）
∴∠1=∠
ACD
（等量代换）
∴EF∥CD（
同位角相等，两直线平行
）
∴∠AEF=∠
ADC
（
两直线平行，同位角相等
）
∵EF⊥AB（已知）
∴∠AEF=90°（
垂直定义
）
∴∠ADC=90°（
等量代换
）
∴CD⊥AB（
垂直定义
）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网