题目内容
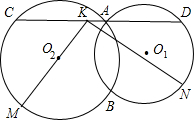 如图,⊙O1与⊙O2相交于点A和B,经过A作直线与⊙O1相交于D,与⊙O2相交于C,设弧BC的中点为M,弧BD的中点为N,线段CD的中点为K.求证:MK⊥KN.
如图,⊙O1与⊙O2相交于点A和B,经过A作直线与⊙O1相交于D,与⊙O2相交于C,设弧BC的中点为M,弧BD的中点为N,线段CD的中点为K.求证:MK⊥KN.
分析:首先将△KDN绕点K顺时针旋转180°得△GCK,连接MC,MB,GC,NB,ND,MN,延长AB交MN于S,根据旋转的性质,即可得CG=DN,∠GCK=∠KDN,又由弧BC的中点为M,弧BD的中点为N,即可证得DN=BN,MC=MB,然后由圆的内接四边形的性质,可证得∠GCM=∠MBN,即可根据SAS证得△GCM≌△NBM,然后由等腰三角形的性质,证得MK⊥KN.
解答: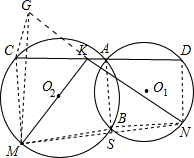 证明:将△KDN绕点K顺时针旋转180°得△GCK,连接MC,MB,GC,NB,ND,MN,延长AB交MN于S.…(3分)
证明:将△KDN绕点K顺时针旋转180°得△GCK,连接MC,MB,GC,NB,ND,MN,延长AB交MN于S.…(3分)
则CG=DN,∠GCK=∠KDN,
∵弧BC的中点为M,弧BD的中点为N,
∴DN=BN,MC=MB,…(6分)
∴CG=BN,
又∵∠KCM=∠MBS,∠GCK=∠KDN=∠SBN,
∴∠GCM=∠MBN,…(9分)
在△GCM与△NBM中,
,
∴△GCM≌△NBM(SAS),…(10分)
∴GM=MN.
又GK=KN,
∴MK⊥KN…(12分)
 证明:将△KDN绕点K顺时针旋转180°得△GCK,连接MC,MB,GC,NB,ND,MN,延长AB交MN于S.…(3分)
证明:将△KDN绕点K顺时针旋转180°得△GCK,连接MC,MB,GC,NB,ND,MN,延长AB交MN于S.…(3分)则CG=DN,∠GCK=∠KDN,
∵弧BC的中点为M,弧BD的中点为N,
∴DN=BN,MC=MB,…(6分)
∴CG=BN,
又∵∠KCM=∠MBS,∠GCK=∠KDN=∠SBN,
∴∠GCM=∠MBN,…(9分)
在△GCM与△NBM中,
|
∴△GCM≌△NBM(SAS),…(10分)
∴GM=MN.
又GK=KN,
∴MK⊥KN…(12分)
点评:此题考查了相交圆的性质,圆的内接四边形的性质,旋转的性质,等腰三角形的判定与性质以及全等三角形的判定与性质等知识.此题综合性很强,难度较大,解题的关键是注意数形结合思想的应用,注意辅助线的作法.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 12、已知:如图,⊙O1与⊙O2外切于点P,直线AB过点P交⊙O1于A,交⊙O2于B,点C、D分别为⊙O1、⊙O2上的点,且∠ACP=65°,则∠BDP=
12、已知:如图,⊙O1与⊙O2外切于点P,直线AB过点P交⊙O1于A,交⊙O2于B,点C、D分别为⊙O1、⊙O2上的点,且∠ACP=65°,则∠BDP=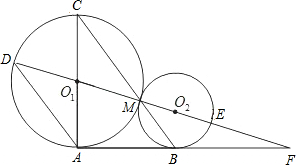 已知:如图,⊙O1与⊙O2外切于M点,AF是两圆的外公切线,A、B是切点,DF经过O1、O2,分别交⊙O1于D、⊙O2于E,AC是⊙O1的直径,BC经过M点,连接AD.
已知:如图,⊙O1与⊙O2外切于M点,AF是两圆的外公切线,A、B是切点,DF经过O1、O2,分别交⊙O1于D、⊙O2于E,AC是⊙O1的直径,BC经过M点,连接AD.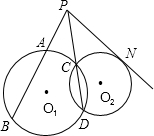 如图,⊙O1与⊙O2相交于C、D两点,⊙O1的割线PAB与DC的延长线交于点P,PN与⊙O2相切于点N,若PB=10,AB=6,则PN=
如图,⊙O1与⊙O2相交于C、D两点,⊙O1的割线PAB与DC的延长线交于点P,PN与⊙O2相切于点N,若PB=10,AB=6,则PN=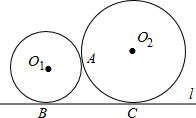 已知:如图,⊙O1与⊙O2外切于A点,直线l与⊙O1、⊙O2分别切于B,C点,若⊙O1的半径r1=2cm,⊙O2的半径r2=3cm.求BC的长.
已知:如图,⊙O1与⊙O2外切于A点,直线l与⊙O1、⊙O2分别切于B,C点,若⊙O1的半径r1=2cm,⊙O2的半径r2=3cm.求BC的长.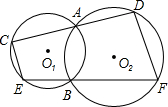 已知如图:⊙O1与⊙O2相交于AB两点,过点A、B的直线分别与⊙O1交于C、E,与⊙O2交于D、F,连接CE、DF.
已知如图:⊙O1与⊙O2相交于AB两点,过点A、B的直线分别与⊙O1交于C、E,与⊙O2交于D、F,连接CE、DF.