题目内容
结果如此巧合!
下面是小颖对一道题目的解答.
题目:如图,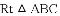
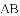
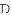
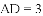
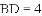
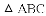
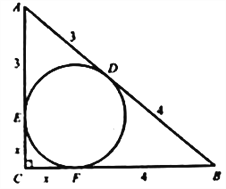
【解析】
设
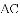
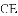
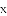
根据切线长定理,得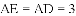
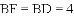
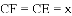
根据勾股定理,得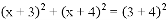 .
.
整理,得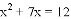 .
.
所以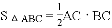
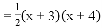
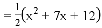
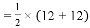
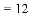
小颖发现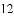
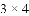
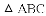
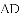
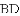
请你帮她完成下面的探索.
已知: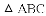
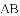
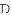
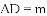
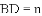
可以一般化吗?
(1)若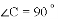 ,求证:
,求证:

倒过来思考呢?
(2)若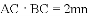
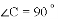 .改变一下条件……
.改变一下条件……
(3)若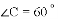 ,用
,用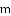
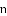
练习册系列答案
相关题目


 B.
B.  C.
C.  D.
D. 
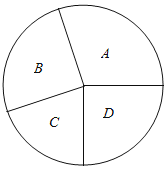
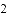
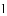
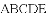
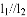 ,则
,则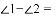
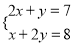 ,那么x+y的值( )
,那么x+y的值( )