题目内容
若a2=1，|b|=5，且ab＜0，则a-b的值为 ．
考点：有理数的乘法,绝对值,有理数的减法,有理数的乘方
专题：
分析：根据有理数的乘方和绝对值的性质求出a、b，再根据异号得负判断出a、b的对应情况，然后代入代数式进行计算即可得解．
解答：解：∵a2=1，|b|=5，
∴a=±1，b=±5，
∵ab＜0，
∴a=1时，b=-5，
a=-1时，b=5，
∴a-b=1-（-5）=1+5=6，
或a-b=-1-5=-6．
故答案为：6或-6．
∴a=±1，b=±5，
∵ab＜0，
∴a=1时，b=-5，
a=-1时，b=5，
∴a-b=1-（-5）=1+5=6，
或a-b=-1-5=-6．
故答案为：6或-6．
点评：本题考查了有理数的乘法，有理数的乘方，绝对值的性质，有理数的减法，熟记运算法则并判断出a、b的对应情况是解题的关键．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
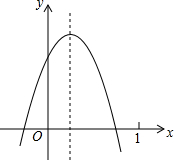已知二次函数y=ax2+bx+c（a≠0）的图象如图，则下列结论：