ЬтФПФкШн
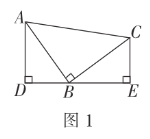
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌОиаЮOABCЕФБпOAдкyжсЕФе§АыжсЩЯЃЌOCдкxжсЕФе§АыжсЩЯЃЌOA=1ЃЌOC=2ЃЌЕуDдкБпOCЩЯЧвOD=1.25ЃЎ

ЃЈ1ЃЉЧѓжБЯпACЕФНтЮіЪНЃЎ
ЃЈ2ЃЉдкyжсЩЯЪЧЗёДцдкЕуPЃЌжБЯпPDгыОиаЮЖдНЧЯпACНЛгкЕуMЃЌЪЙЕУЁїDMCЮЊЕШбќШ§НЧаЮЃПШєДцдкЃЌжБНгаДГіЫљгаЗћКЯЬѕМўЕФЕуPЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЃЈ3ЃЉХзЮяЯпy=Љx2ОЙ§дѕбљЦНвЦЃЌВХФмЪЙЕУЦНвЦКѓЕФХзЮяЯпЙ§ЕуDКЭЕуEЃЈЕуEдкyжсе§АыжсЩЯЃЉЃЌЧвЁїODEбиDEелЕўКѓЕуOТфдкБпABЩЯOЁфДІЃП
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉPЕузјБъЮЊЃЈ0ЃЌ
ЃЛЃЈ2ЃЉPЕузјБъЮЊЃЈ0ЃЌ ![]() ЃЉЛђЃЈ0ЃЌЉ
ЃЉЛђЃЈ0ЃЌЉ![]() ЃЉЛђЃЈ0ЃЌ
ЃЉЛђЃЈ0ЃЌ ![]() ЃЉЛђЃЈ0ЃЌ
ЃЉЛђЃЈ0ЃЌ ![]() ЃЉЃЛ ЃЈ3ЃЉХзЮяЯпy=Љx2ЯШЯђгв
ЃЉЃЛ ЃЈ3ЃЉХзЮяЯпy=Љx2ЯШЯђгв![]() ЕЅЮЛЃЌдйЯђЩЯЦНвЦ
ЕЅЮЛЃЌдйЯђЩЯЦНвЦ![]() ЕЅЮЛЃЌВХФмЪЙЕУЦНвЦКѓЕФХзЮяЯпЙ§ЕуDКЭЕуEЃЎ
ЕЅЮЛЃЌВХФмЪЙЕУЦНвЦКѓЕФХзЮяЯпЙ§ЕуDКЭЕуEЃЎ
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉЯШШЗЖЈ![]() ЕуКЭ
ЕуКЭ![]() ЕузјБъЃЌШЛКѓРћгУД§ЖЈЯЕЪ§ЗЈЧѓжБЯп
ЕузјБъЃЌШЛКѓРћгУД§ЖЈЯЕЪ§ЗЈЧѓжБЯп![]() ЕФНтЮіЪНЃЛ
ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЩш![]() ЬжТлЃКЕБ
ЬжТлЃКЕБ![]() ЪБЃЌ
ЪБЃЌ ![]() НтЗНГЬЧѓГі
НтЗНГЬЧѓГі![]() ЃЌдйЧѓГі
ЃЌдйЧѓГі![]() ЕФНтЮіЪНЃЌДгЖјЕУЕН
ЕФНтЮіЪНЃЌДгЖјЕУЕН![]() ЕузјБъЃЛЕБ
ЕузјБъЃЛЕБ![]() ЪБЃЌвзЕУ
ЪБЃЌвзЕУ![]() ЕуЕФзјБъЃЌНгзХЧѓГі
ЕуЕФзјБъЃЌНгзХЧѓГі![]() ЕФНтЮіЪНЃЌДгЖјЕУЕН
ЕФНтЮіЪНЃЌДгЖјЕУЕН![]() ЕузјБъЃЛЕБCM=CDЪБ,
ЕузјБъЃЛЕБCM=CDЪБ, ![]() НтЗНГЬЧѓГі
НтЗНГЬЧѓГі![]() ЃЌдйШЗЖЈ
ЃЌдйШЗЖЈ![]() ЕФНтЮіЪНЃЌДгЖјЕУЕН
ЕФНтЮіЪНЃЌДгЖјЕУЕН![]() ЕузјБъЃЛ
ЕузјБъЃЛ
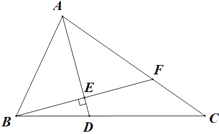
ЃЈ3ЃЉШчЭМ2ЃЌзїOЁфHЁЭxжсгкH,дђ![]() ЩшOЁф(m,1)ЃЌРћгУЙДЙЩЖЈРэЕУЕФ
ЩшOЁф(m,1)ЃЌРћгУЙДЙЩЖЈРэЕУЕФ![]() ,НтЕУ
,НтЕУ![]() ЕБm=2ЪБЃЌЧѓГі
ЕБm=2ЪБЃЌЧѓГі![]() ГЄЕУЕН
ГЄЕУЕН![]() РћгУД§ЖЈЯЕЪ§ЗЈЧѓГіХзЮяЯпНтЮіЪНЮЊ
РћгУД§ЖЈЯЕЪ§ЗЈЧѓГіХзЮяЯпНтЮіЪНЮЊ![]() ШЛКѓРћгУХзЮяЯпЕФЦНвЦБфЛЛЧѓНтЃЛЕБ
ШЛКѓРћгУХзЮяЯпЕФЦНвЦБфЛЛЧѓНтЃЛЕБ![]() ЪБЃЌЭЌбљПЩЕУХзЮяЯпНтЮіЪНЮЊ
ЪБЃЌЭЌбљПЩЕУХзЮяЯпНтЮіЪНЮЊ![]() дйРћгУХзЮяЯпЕФЦНвЦБфЛЛЧѓНтЃЎ
дйРћгУХзЮяЯпЕФЦНвЦБфЛЛЧѓНтЃЎ
ЪдЬтНтЮіЃК(1)ЁпOA=1,OC=2,
ЁрA(0,1),C(2,0)ЃЌ
ЩшжБЯпACЕФНтЮіЪНЮЊy=kx+bЃЌ
АбA(0,1),C(2,0)ДњШыЕУ![]() НтЕУ
НтЕУ
ЁржБЯпACЕФНтЮіЪНЮЊ![]()
(2)Дцдк.

![]()
Щш![]()
ЕБDM=DCЪБ, ![]() НтЕУ
НтЕУ![]() (ЩсШЅ),дђ
(ЩсШЅ),дђ![]() ,ДЫЪБMDЕФНтЮіЪНЮЊ
,ДЫЪБMDЕФНтЮіЪНЮЊ![]() PЕузјБъЮЊ
PЕузјБъЮЊ![]()
ЕБMD=MCЪБ,дђMЕуЕФзјБъЮЊ![]() ДЫЪБMDЕФНтЮіЪНЮЊ
ДЫЪБMDЕФНтЮіЪНЮЊ![]() PЕузјБъЮЊ
PЕузјБъЮЊ![]()
ЕБCM=CDЪБ, ![]() НтЕУ
НтЕУ![]()
дђ Лђ
Лђ
ДЫЪБMDЕФНтЮіЪНЮЊ Лђ
Лђ PЕузјБъЮЊ
PЕузјБъЮЊ Лђ
Лђ
злЩЯЫљЪі,PЕузјБъЮЊ![]() Лђ
Лђ![]() Лђ
Лђ Лђ
Лђ ;
;
(3)ЁїODEбиDEелЕўКѓЕуOТфдкБпABЩЯOЁфДІ,ШчЭМ2,зїOЁфHЁЭxжсгкH,дђ![]()
ЩшOЁф(m,1)ЃЌ
дк![]() жа,
жа, ![]() , НтЕУ
, НтЕУ![]()
ЕБm=2ЪБ,AOЁф=2,ЖјEOЁф=EO=EA+1ЃЌ
![]() ,НтЕУ
,НтЕУ![]()
![]()
ЩшЦНвЦЕФХзЮяЯпНтЮіЪНЮЊ![]()
Аб![]() ДњШыЕУ
ДњШыЕУ НтЕУ
НтЕУ
ЁрХзЮяЯпНтЮіЪНЮЊ![]()
![]()
ЁрХзЮяЯп![]() ЯШЯђзѓ
ЯШЯђзѓ![]() ЕЅЮЛ,дйЯђЩЯЦНвЦ
ЕЅЮЛ,дйЯђЩЯЦНвЦ![]() ЕЅЮЛЃЌВХФмЪЙЕУЦНвЦКѓЕФХзЮяЯпЙ§ЕуDКЭЕуEЃЛ
ЕЅЮЛЃЌВХФмЪЙЕУЦНвЦКѓЕФХзЮяЯпЙ§ЕуDКЭЕуEЃЛ
ЕБ![]() ЪБ,
ЪБ, ![]() ,ЖјEOЁф=EO=1AEЃЌ
,ЖјEOЁф=EO=1AEЃЌ
![]() НтЕУ
НтЕУ![]()
![]()
ЭЌбљПЩЕУХзЮяЯпНтЮіЪНЮЊ![]()
![]()
ЁрХзЮяЯп![]() ЯШЯђгв
ЯШЯђгв![]() ЕЅЮЛ,дйЯђЩЯЦНвЦ
ЕЅЮЛ,дйЯђЩЯЦНвЦ![]() ЕЅЮЛЃЌВХФмЪЙЕУЦНвЦКѓЕФХзЮяЯпЙ§ЕуDКЭЕуE.
ЕЅЮЛЃЌВХФмЪЙЕУЦНвЦКѓЕФХзЮяЯпЙ§ЕуDКЭЕуE.

 МЄЛюЫМЮЌгХМгПЮЬУЯЕСаД№АИ
МЄЛюЫМЮЌгХМгПЮЬУЯЕСаД№АИ ЛюСІЪдОэЯЕСаД№АИ
ЛюСІЪдОэЯЕСаД№АИЁОЬтФПЁПЮЊСЫНтОХФъМЖбЇЩњЕФЬхФмЧщПіЃЌбЇаЃзщжЏСЫвЛДЮЬхФмВтЪдЃЌВЂЫцЛњбЁШЁ50УћбЇЩњЕФГЩМЈНјааЭГМЦЃЌЕУГіЯрЙиЭГМЦБэКЭЭГМЦЭМ(ЦфжаВПЗжЪ§ОнВЛЩїЖЊЪЇЃЌднгУзжФИmЃЌnБэЪО).
ГЩМЈЕШМЖ | гХау | СМКУ | КЯИё | ВЛКЯИё |
ШЫЪ§ | m | 30 | n | 5 |
ЧыИљОнЭМБэЫљЬсЙЉЕФаХЯЂЛиД№ЯТСаЮЪЬтЃК
(1)ЭГМЦБэжаЕФmЃН ЃЌnЃН ЃЛВЂВЙШЋЦЕЪ§ЗжВМжБЗНЭМЃЛ
(2)ШєИУаЃОХФъМЖга500УћбЇЩњЃЌЧыОнДЫЙРМЦИУаЃОХФъМЖбЇЩњЬхФмСМКУМАСМКУвдЩЯЕФбЇЩњгаЖрЩйШЫЃП