Question

已知：如图，钝角△ABC中，∠A为钝角，∠B=30°，AB=6，AC=5．求△ABC的面积．（结果保留根号）

Answer 1

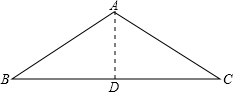解：过点A作AD⊥BC于D，
∵∠B=30°，AB=6，
∴，
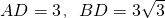在Rt△ACD中，∵AD⊥BC，
∴．
∴．
∴．
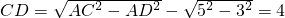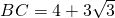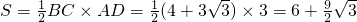分析：过点A作AD⊥BC于D，可分成两个直角三角形，因为∠B=30°，可求出AD，BD的长，根据勾股定理求出CD的长，从而求出BC的长，根据三角形的面积公式可求解．
点评：本题考查勾股定理的应用，和直角三角形中，30°角所对的边是斜边的一半，求出各线段的长，根据三角形的面积公式可求解．