题目内容
【题目】小明为探究函数
的图象和性质，需要画出函数图象，列表如下：
| …… |
|
|
|
|
|
|
|
|
|
| …… |
| …… |
|
|
|
|
|
|
|
|
|
| …… |
根据上表数据，在平面直角坐标系中描点，画出函数图象，如图如示，小明画出了图象的一部分．
（1）请你帮小明画出完整的的图象；
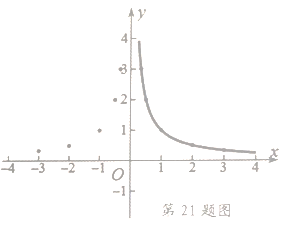
（2）观察函数图象，请写出这个函数的两条性质：
性质一： ；
性质二： ．
（3）利用上述图象，探究函数图象与直线
的关系；
①当
时， 直线与函数在第一象限的图象有一个交点
，则的坐标是 ；
②当
为何值时，讨论函数的图象与直线的交点个数．
【答案】（1）见解析；（2）性质一：图象有两个分支，分别在第一、第二象限；性质二：图象在第一象限时，y随x的增大而减小，在第二象限时，y随x的增大而增大；（3）①当b=2，A(1，1)，②当b＞2时，两个函数有三个交点；当b=2时，两个函数有两个交点；当b＜2时，两函数有一个交点
【解析】
（1）根据表格描点，连线即可；
（2）根据图象观察即可得出结论；
（3）①当x>0时，方程-x+b=
，整理得x2-bx+1=0，根据直线y=-x+b与函数
的图象在第一象限只有一个交点，可得
=0，解得b=2，把b=2代入x2-bx+1=0，即可的到点A的坐标；
②由一次函数的性质可得
的图象经过必定经过二、四象限，所以当x<0时，直线y=-x+b与函数的图象在第二象限只有一个交点，再结合图象讨论当x>0时的情况，即可得出答案．
解：（1）绘制完整图象如下图：
；
（2）由图象可得：图象有两个分支，分别在第一、第二象限；
图象在第一象限时，y随x的增大而减小，在第二象限时，y随x的增大而增大；
（3）①当x>0时，方程-x+b=，即为-x+b=
，
整理得x2-bx+1=0，
∵直线y=-x+b与函数的图象在第一象限只有一个交点，
∴=0，即b2-4=0，
解得b=2，b=-2（不符合题意，舍去），
把b=2代入x2-bx+1=0，
解得x1=x2=1，
故点A的坐标为（1，1）；
②∵的k值小于0，
∴图象经过必定经过二、四象限，
∴当x<0时，直线y=-x+b与函数的图象在第二象限只有一个交点，
由①可知，当x>0，b=2时，直线y=-x+b与函数的图象在第一象限只有一个交点，
∴当b=2时，两个函数有两个交点，
结合图象可知当b＞2时，两个函数有三个交点，当b＜2时，两函数有一个交点，
综上：当b＞2时，两个函数有三个交点；当b=2时，两个函数有两个交点当b＜2时；两函数有一个交点．
