��Ŀ����
��14�֣���ͼ����ƽ��ֱ������ϵ�У�������y=mx2��8mx+4m+2��m��2����y��Ľ���ΪA����x��Ľ���ֱ�ΪB��x1��0����C��x2��0������x2��x1=4��ֱ��AD��x�ᣬ��x������һ����E��t��0������E��ƽ����y���ֱ��l�������ߡ�ֱ��AD�Ľ���ֱ�ΪP��Q��
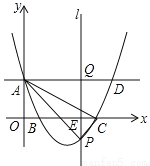
��1���������ߵĽ���ʽ��
��2����0��t��8ʱ�����APC��������ֵ��
��3����t��2ʱ���Ƿ���ڵ�P��ʹ��A��P��QΪ��������������AOB���ƣ������ڣ������ʱt��ֵ���������ڣ���˵�����ɣ�
��1������2��12����3��t=��t=��t=14�� �������������������1���������ø���ϵ���Ĺ�ϵ�ó��� ��������������ֵ��Ȼ��ѵ�B��C������������ʽ���㼴�ɣ���2����2����0��t��6ʱ��6��t��8ʱ��������������ۣ��ݴ˼�����������ε����ֵ����3����3����2��t��6ʱ��t��6ʱ��������������ۣ��ٸ������������Ƶ����������ɵý⣮ ����������������� ��1��������֪x1��x2��...
��ϰ��ϵ�д�
 ��ѧ��ʦ����ϵ�д�
��ѧ��ʦ����ϵ�д�
�����Ŀ
2014�괺���ڼ����г��������������������ʾ��1��30����2��6���ڼ䣬���п���������Ϊ����������Ⱦָ�����±���
���� | 30�� | 31�� | 1�� | 2�� | 3�� | 4�� | 5�� | 6�� |
��Ⱦָ�� | 91 | 96 | 82 | 85 | 80 | 56 | 72 | 62 |
���������ݵ���λ����ƽ�����ֱ�Ϊ_____��
81��78 ���������������ݰ��մ�С�����˳������Ϊ��56��62��72��80��82��85��91��96�� ���������ݵ���λ��Ϊ�� �� ƽ����Ϊ�� �� �ʴ�Ϊ��81��78��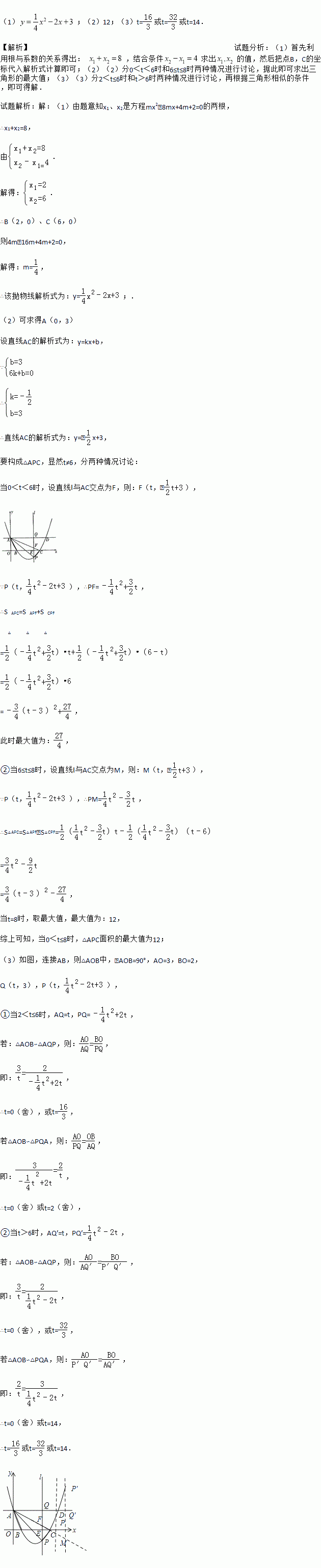

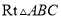 �У�
�� 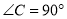 ��
�� 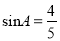 ��
�� 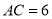 ����ô
����ô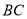 ���ڣ� ����
���ڣ� ����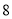 B.
B. 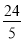 C.
C. 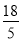 D.
D. 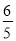
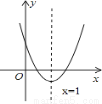
 x��2��x��
x��2��x��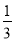 y��+����
y��+����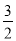 x+
x+ 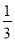 y��������x=��2��y=
y��������x=��2��y=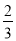 ��
��