题目内容
如图，四边形ABCD是边长为1 的正方形，四边形EFGH是边长为2的正方形，点D与点F重合，点B，D（F），H在同一条直线上，将正方形ABCD沿F→H方向平移至点B与点H重合时停止，设点D、F之间的距离为x，正方形ABCD与正方形EFGH重叠部分的面积为y，则能大致反映y与 x之间函数关系的图象是（ ）
B
试题分析：重叠部分为正方形，
，当
时，此时，重叠部分面积为
，即函数图象为抛物线
中时的图象，面积最大值1；为当
，此时重叠面积固定，为小正方形面积，面积为1；当
，此时重叠部分面积为
，即函数图象为抛物线
中时的图象，面积最小为0，综上，可以知道为B选项点评：此题要观察函数的变化，可以用分段函数概括
练习册系列答案
相关题目
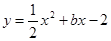与x轴交于A，B两点，与y轴交于C点，且A（﹣1，0）．
的图象经过A（2，0）、B（0，－6）两点。
轴交于点C，连结BA、BC，求△ABC的面积。
的图象和性质．
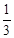
的图象上有A（
，
），B（
，
），C（2，
）三个点，则
，
是不为0的常数．
的右侧，求
的图象如图，若一元二次方程
的结论正确的是（ ）