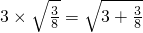题目内容
观察下列式子 ,
, ,
, …根据上述规律计算:
…根据上述规律计算: ,并求出当a=2011时,上式的值.
,并求出当a=2011时,上式的值.
解:∵当n=1时, ,
,
当n=2时, ,
,
当n=3时, ,
,
…
∴当n=n时,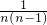 =
= -
- .
.
∴
=a( +
+ +
+ +…+
+…+ )
)
=a(1- +
+ -
- +
+ -
- +…+
+…+ -
- )
)
=a(1- )
)
= a,
a,
当a=2011时,原式= ×2011=2010.
×2011=2010.
分析:先由已知等式,得出规律: =
= -
- ,再将所求式子提取公因式a,变形为a(
,再将所求式子提取公因式a,变形为a( +
+ +
+ +…+
+…+ ),然后利用得出的规律,化简括号内的式子,最后将a=2011代入,计算即可求解.
),然后利用得出的规律,化简括号内的式子,最后将a=2011代入,计算即可求解.
点评:此题主要考查了规律型:数字的变化类及有理数的混合运算,解题时首先观察,分析归纳出题目中隐含的规律,然后利用规律把题目变形,从而使计算变得比较简便.
 ,
,当n=2时,
 ,
,当n=3时,
 ,
,…
∴当n=n时,
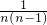 =
= -
- .
.∴

=a(
 +
+ +
+ +…+
+…+ )
)=a(1-
 +
+ -
- +
+ -
- +…+
+…+ -
- )
)=a(1-
 )
)=
 a,
a,当a=2011时,原式=
 ×2011=2010.
×2011=2010.分析:先由已知等式,得出规律:
 =
= -
- ,再将所求式子提取公因式a,变形为a(
,再将所求式子提取公因式a,变形为a( +
+ +
+ +…+
+…+ ),然后利用得出的规律,化简括号内的式子,最后将a=2011代入,计算即可求解.
),然后利用得出的规律,化简括号内的式子,最后将a=2011代入,计算即可求解.点评:此题主要考查了规律型:数字的变化类及有理数的混合运算,解题时首先观察,分析归纳出题目中隐含的规律,然后利用规律把题目变形,从而使计算变得比较简便.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
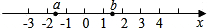



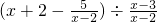 ,其中
,其中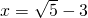 ;
; ,先化简再求
,先化简再求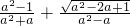 的值;
的值;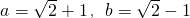 ,求a2-a2005b2006+b2的值;
,求a2-a2005b2006+b2的值;
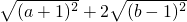 -|a-b|;
-|a-b|;