题目内容
1.不解方程,判断方程的实数根的个数:(1)x2+x-1=0;
(2)x2-4x+4=0;
(3)x2-x+1=0.
分析 (1)根据方程的系数结合根的判别式,可得出△=5>0,由此可得出原方程有两个不相等的实数根;
(2)根据方程的系数结合根的判别式,可得出△=0,由此可得出原方程有两个相等的实数根;
(3)根据方程的系数结合根的判别式,可得出△=-3<0,由此可得出原方程,没有实数根.
解答 解:(1)∵△=12-4×1×(-1)=5>0,
∴方程x2+x-1=0有两个不相等的实数根;
(2)∵△=(-4)2-4×1×4=0,
∴方程x2-4x+4=0有两个相等的实数根;
(3)∵△=(-1)2-4×1×1=-3<0,
∴方程x2-x+1=0没有实数根.
点评 本题考查了根的判别式,牢记“当△>0时,方程有两个不相等的实数根;当△=0时,方程有两个相等的实数根;当△<0时,方程无实数根.”是解题的关键.

练习册系列答案
相关题目
 如图是某养鸡场2005~2010年的养鸡统计图:
如图是某养鸡场2005~2010年的养鸡统计图: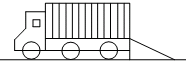 如图,货车卸货时支架侧面是Rt△ABC,其中∠ACB=90°,已知AB=2.5m,AC=2m,则BC的长为1.5m.
如图,货车卸货时支架侧面是Rt△ABC,其中∠ACB=90°,已知AB=2.5m,AC=2m,则BC的长为1.5m. 如图,△ABC中,AB=6,BC=8,AC=4,点D、E分别在边AB、AC上,DE的延长线与BC的延长线相交于点F,且$\frac{AD}{AE}$=$\frac{2}{3}$.
如图,△ABC中,AB=6,BC=8,AC=4,点D、E分别在边AB、AC上,DE的延长线与BC的延长线相交于点F,且$\frac{AD}{AE}$=$\frac{2}{3}$.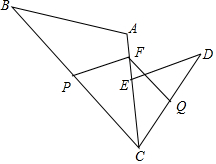 如图:E、A、C三点在同一条直线上,三角形ABC和三角形CDE是顶角相等的等腰三角形,其中BC和CD为等腰三角形的底边,F是AE的中点,P是BC边的中点,Q是CD边的中点.
如图:E、A、C三点在同一条直线上,三角形ABC和三角形CDE是顶角相等的等腰三角形,其中BC和CD为等腰三角形的底边,F是AE的中点,P是BC边的中点,Q是CD边的中点.