题目内容
 已知直线l过(1,3)和(3,1)两点,且与x轴,y轴分别交于点A,B,
已知直线l过(1,3)和(3,1)两点,且与x轴,y轴分别交于点A,B,
(1)求直线l的函数关系式yAB;
(2)在图中,画出直线l;
(3)求△AOB的面积;
(4)当x________时,yAB>0.
解:(1)设求直线l的函数关系式yAB=kx+b(k≠0).
∵直线l过(1,3)和(3,1)两点,
∴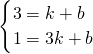 ,
,
解得,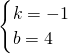 ,
,
∴直线l的函数关系式为:yAB=-x+4;
(2)当x=0时,y=4;
当y=0时,x=4,
∴A(4,0)、B(0,4)
∴直线l如图所示:
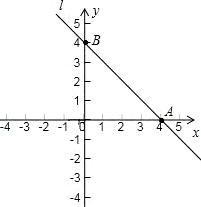
(3)S△AOB= ×OA•OB=
×OA•OB= ×4×4=8,即S△AOB=8;
×4×4=8,即S△AOB=8;
(4)根据图示知,当x<4时,yAB>0.
故答案为:<4.
分析:(1)利用待定系数法求一次函数解析式;
(2)根据(1)的解析式,求出点A、B的坐标,然后连接AB即可;
(3)根据三角形的面积公式面积= ×底×高;
×底×高;
(4)根据图示,直接回答.
点评:本题主要考查的是用待定系数法求一次函数解析式及一次函数图象.解答此题的关键是根据一次函数图象与坐标特征求的一次函数的解析式.
∵直线l过(1,3)和(3,1)两点,
∴
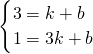 ,
,解得,
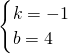 ,
,∴直线l的函数关系式为:yAB=-x+4;
(2)当x=0时,y=4;
当y=0时,x=4,
∴A(4,0)、B(0,4)
∴直线l如图所示:
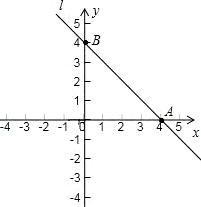
(3)S△AOB=
 ×OA•OB=
×OA•OB= ×4×4=8,即S△AOB=8;
×4×4=8,即S△AOB=8;(4)根据图示知,当x<4时,yAB>0.
故答案为:<4.
分析:(1)利用待定系数法求一次函数解析式;
(2)根据(1)的解析式,求出点A、B的坐标,然后连接AB即可;
(3)根据三角形的面积公式面积=
 ×底×高;
×底×高;(4)根据图示,直接回答.
点评:本题主要考查的是用待定系数法求一次函数解析式及一次函数图象.解答此题的关键是根据一次函数图象与坐标特征求的一次函数的解析式.

练习册系列答案
相关题目
 三角形?若存在,求出点C的坐标,并证明;若不存在,请说明理由.
三角形?若存在,求出点C的坐标,并证明;若不存在,请说明理由.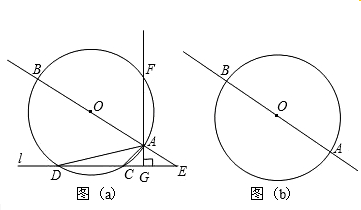
 如图,已知直线l过A(4,0)、B(0,4)两点,它与二次函数y=ax2的图象在第一象限内相交于点P.若△AOP的面积为
如图,已知直线l过A(4,0)、B(0,4)两点,它与二次函数y=ax2的图象在第一象限内相交于点P.若△AOP的面积为