题目内容
10.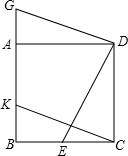 如图,四边形ABCD是正方形,点E、K分别在BC、AB上,且CE=BK,并将△DCE绕点D顺时针旋转90°得到△DAG.
如图,四边形ABCD是正方形,点E、K分别在BC、AB上,且CE=BK,并将△DCE绕点D顺时针旋转90°得到△DAG.(1)尺规作图,以线段DE,DG为边作出正方形DEFG(要求:要求保留作图痕迹,不用写作法和证明);
(2)连接(1)中的KF,求证:四边形CEFK是平行四边形;
(3)当tan∠BCK=$\frac{1}{3}$时,求$\frac{{S}_{正方形ABCD}}{{S}_{正方形DEFG}}$的值.
分析 (1)分别过E和G作DE和DG的垂线,交点是F,即可求解;
(2)证明△BCK≌△CDE,证明∠EGC=90°,则CK∥EF且CK=EF即可证得;
(3)根据三角函数求得BC和CK的比值,即两个正方形的边长的比,进而求得面积的比.
解答 解:(1)如图: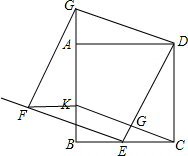
四边形CEFK是所求的四边形;
(2)∵在直角△BCK和直角△CDE中,
$\left\{\begin{array}{l}{EC=KB}\\{CD=BC}\end{array}\right.$,
∴△BCK≌△CDE,
∴DE=CK,∠BCK=∠CDE,
又∵直角△CDE中,∠DEC+∠CDE=90°,
∴∠DEC+∠BCK=90°,
∴∠EGC=90°,
又∵正方形DEFG中,∠DEF=90°,
∴CK∥EF,
又∵EF=DE,
∴EF=CK,
∴四边形DEFG是平行四边形;
(3)∵tan∠BCK=$\frac{1}{3}$,
∴cos∠BCK=$\frac{3\sqrt{10}}{10}$.
∴$\frac{{S}_{正方形ABCD}}{{S}_{正方形DEFG}}$=(cos∠BCK)2=($\frac{3\sqrt{10}}{10}$)2=$\frac{9}{10}$.
点评 本题考查了正方形的性质以及平行四边形的判定,正确证明CK∥EF是解决本题的关键.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案
相关题目
18.9的算术平方根是( )
| A. | 81 | B. | 3 | C. | -3 | D. | ±3 |
15.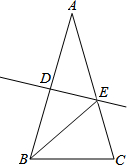 如图,AB=AC,∠A=40°,AB的垂直平分线DE交AC于点E,垂足为D,则∠EBC的度数是( )
如图,AB=AC,∠A=40°,AB的垂直平分线DE交AC于点E,垂足为D,则∠EBC的度数是( )
 如图,AB=AC,∠A=40°,AB的垂直平分线DE交AC于点E,垂足为D,则∠EBC的度数是( )
如图,AB=AC,∠A=40°,AB的垂直平分线DE交AC于点E,垂足为D,则∠EBC的度数是( )| A. | 30° | B. | 40° | C. | 70° | D. | 80° |
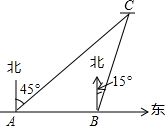 如图,有A、B两艘船在大海中航行,B船在A船的正东方向,且两船保持20海里的距离,某一时刻这两艘船同时测得在A的东北方向,B的北偏东15°方向有另一艘船C,那么此时船C与船B的距离是20$\sqrt{2}$海里.(结果保留根号)
如图,有A、B两艘船在大海中航行,B船在A船的正东方向,且两船保持20海里的距离,某一时刻这两艘船同时测得在A的东北方向,B的北偏东15°方向有另一艘船C,那么此时船C与船B的距离是20$\sqrt{2}$海里.(结果保留根号)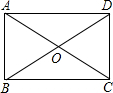 如图,矩形ABCD的对角线AC、BD交于点O,∠AOB=60°,AB=3,求BD的长.
如图,矩形ABCD的对角线AC、BD交于点O,∠AOB=60°,AB=3,求BD的长.