题目内容
1.已知|x|=$\frac{1}{6}$,|y|=4,且x>y,求代数式3x-$\frac{1}{2}$y的值.分析 根据绝对值的性质即可求出x与y的值,然后分情况求出原式的值.
解答 解:由题意可知:x=$±\frac{1}{6}$,y=±4,
∵x>y,
∴x=±$\frac{1}{6}$,y=-4,
当x=$\frac{1}{6}$,y=-4时,
原式=3×$\frac{1}{6}$-$\frac{1}{2}$×(-4)=2$\frac{1}{2}$,
当x=-$\frac{1}{6}$,y=-4时,
原式=3×(-$\frac{1}{6}$)-$\frac{1}{2}$×(-4)=1$\frac{1}{2}$
综上所述,3x-$\frac{1}{2}$y的值为2$\frac{1}{2}$或1$\frac{1}{2}$
点评 本题考查代入式求值问题,涉及绝对值的性质,分类讨论的思想.

练习册系列答案
相关题目
12.若$\frac{a}{b}$=$\frac{2}{3}$,则$\frac{a}{a+b}$等于( )
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
9.将抛物线y=x2-2x+3平移得到抛物线y=x2,则这个平移过程正确的是( )
| A. | 先向左平移1个单位,再向下平移2个单位 | |
| B. | 先向左平移2个单位,再向下平移1个单位 | |
| C. | 先向右平移1个单位,再向上平移2个单位 | |
| D. | 先向右平移2个单位,再向上平移1个单位 |
16.下列代数式书写正确的是( )
| A. | b÷2a2 | B. | 1$\frac{1}{2}$a2 | C. | -$\frac{3}{2}$a2×b | D. | $\frac{b}{2{a}^{2}}$ |
6.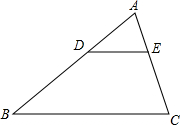 如图,△ADE∽△ABC,若AD=2,BD=4,则△ADE与△ABC的相似比是( )
如图,△ADE∽△ABC,若AD=2,BD=4,则△ADE与△ABC的相似比是( )
 如图,△ADE∽△ABC,若AD=2,BD=4,则△ADE与△ABC的相似比是( )
如图,△ADE∽△ABC,若AD=2,BD=4,则△ADE与△ABC的相似比是( )| A. | 1:2 | B. | 1:3 | C. | 2:3 | D. | 3:2 |
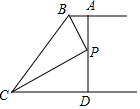 如图,AB∥CD,BP和CP分别平分∠ABC和∠DCB,AD过点P,且与AB垂直,若AD=8,则点P到BC的距离是( )
如图,AB∥CD,BP和CP分别平分∠ABC和∠DCB,AD过点P,且与AB垂直,若AD=8,则点P到BC的距离是( ) 如图,已知菱形ABCD的边长是13,O是对角线的交点,过O点的三条直线将菱形分成阴影和空白部分.若菱形一条对角线长为10,则图中阴影部分的面积为60.
如图,已知菱形ABCD的边长是13,O是对角线的交点,过O点的三条直线将菱形分成阴影和空白部分.若菱形一条对角线长为10,则图中阴影部分的面积为60.