题目内容
19.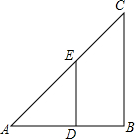 如图所示,已知△ABC∽△ADE,AE=50cm,EC=30cm,BC=56.8cm,∠A=45°,∠ACB=40°,求
如图所示,已知△ABC∽△ADE,AE=50cm,EC=30cm,BC=56.8cm,∠A=45°,∠ACB=40°,求(1)∠AED和∠ADE的度数;
(2)DE的长.
分析 (1)根据三角形的内角和定理求出∠ABC的度数,根据相似三角形的性质求出∠AED和∠ADE的度数;
(2)根据相似三角形对应边的比相等解答.
解答 解:(1)∵∠A=45°,∠ACB=40°,
∴∠ABC=95°,
∵△ABC∽△ADE,
∴∠AED=∠ACB=40°,
∠ADE=∠ABC=95°;
(2)∵△ABC∽△ADE,
∴$\frac{DE}{BC}$=$\frac{AE}{AC}$=$\frac{5}{8}$,
又∵BC=56.8cm,
∴DE=35.5cm.
点评 本题考查的是相似三角形的性质,掌握相似三角形的对应角相等,对应边的比相等是解题的关键.

练习册系列答案
相关题目
9.下列说法中,正确的是( )
| A. | 0是最小的整数 | B. | 互为相反数的两个数之和为零 | ||
| C. | 有理数包括正有理数和负有理数 | D. | 一个有理数的平方总是正数 |
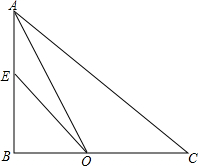 在△ABC中,∠ABC=90°,∠A的平分线AO交BC于O点,将线段OC绕点O逆时针旋转,使点C恰好落在边AB上E点处
在△ABC中,∠ABC=90°,∠A的平分线AO交BC于O点,将线段OC绕点O逆时针旋转,使点C恰好落在边AB上E点处  如图,由两个全等的梯形可以拼成一个菱形吗?符合什么条件的两个全等梯形可以凭此一个菱形?
如图,由两个全等的梯形可以拼成一个菱形吗?符合什么条件的两个全等梯形可以凭此一个菱形?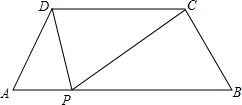 如图,梯形ABCD中,AB∥CD,AD=BC,∠A=60°,AD=4,CD=6,动点P从点A出发,沿AB方向以2单位长度/秒的速度向终点B运动,连接PC,PD,设点P运动的时间为t秒.
如图,梯形ABCD中,AB∥CD,AD=BC,∠A=60°,AD=4,CD=6,动点P从点A出发,沿AB方向以2单位长度/秒的速度向终点B运动,连接PC,PD,设点P运动的时间为t秒.