题目内容
(1)
(2)-42+(-7+5)2×(-1)4
(3)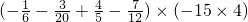
(4)
解:(1)原式=2×9-26×(-2),
=18+52,
=70;
(2)原式=-16+4×1=-12;
(3)原式=(- )×(-60)+(-
)×(-60)+(- )×(-60)+
)×(-60)+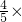 (-60)+(-
(-60)+(- )×(-60),
)×(-60),
=10+9-48+35,
=6;
(4)原式=1-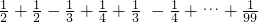 -
- ,
,
=1- ,
,
= .
.
分析:(1)结合运算顺序,利用有理数的运算性质即可解决,
(2)结合运算顺序,以及幂的乘方,利用有理数的运算性质即可解决,
(3)结合运算顺序,以及异分母有理数的运算,利用有理数的运算性质即可解决,
(4)结合数据特殊性将每个分数变成立两个式子相减的形式,即可解决.
点评:此题主要考查了有理数的运算法则,以及特殊有理数的运算应借助于规律解决.
=18+52,
=70;
(2)原式=-16+4×1=-12;
(3)原式=(-
 )×(-60)+(-
)×(-60)+(- )×(-60)+
)×(-60)+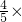 (-60)+(-
(-60)+(- )×(-60),
)×(-60),=10+9-48+35,
=6;
(4)原式=1-
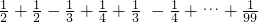 -
- ,
,=1-
 ,
,=
 .
.分析:(1)结合运算顺序,利用有理数的运算性质即可解决,
(2)结合运算顺序,以及幂的乘方,利用有理数的运算性质即可解决,
(3)结合运算顺序,以及异分母有理数的运算,利用有理数的运算性质即可解决,
(4)结合数据特殊性将每个分数变成立两个式子相减的形式,即可解决.
点评:此题主要考查了有理数的运算法则,以及特殊有理数的运算应借助于规律解决.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2010年6月5日是第38个世界环境日,世界环境日的主题为“多个物种、一颗星球、一个未来”.为了响应节能减排的号召,某品牌汽车4S店准备购进A型(电动汽车)和B型(太阳能汽车)两种不同型号的汽车共16辆,以满足广大支持环保的购车者的需求.市场营销人员经过市场调查得到如下信息:
(1)若经营者的购买资金不少于576万元且不多于600万元,则有哪几种进车方案?
(2)在(1)的前提下,如果你是经营者,并且所进的汽车能全部售出,你会选择哪种进车方案才能使获得的利润最大?最大利润是多少?
(3)假设每台电动汽车每公里的用电费用为0.65元,且两种汽车最大行驶里程均为30万公里,那么从节约资金的角度,你做为一名购车者,将会选购哪一种型号的汽车?并说明理由.
| 成本价(万元/辆) | 售价(万元/辆) | |
| A型 | 30 | 32 |
| B型 | 42 | 45 |
(2)在(1)的前提下,如果你是经营者,并且所进的汽车能全部售出,你会选择哪种进车方案才能使获得的利润最大?最大利润是多少?
(3)假设每台电动汽车每公里的用电费用为0.65元,且两种汽车最大行驶里程均为30万公里,那么从节约资金的角度,你做为一名购车者,将会选购哪一种型号的汽车?并说明理由.
 如图,四边形ABCD中,∠ABC=90°,AB=3,BC=4,CD=12,AD=13,则四边形ABCD的面积为( )
如图,四边形ABCD中,∠ABC=90°,AB=3,BC=4,CD=12,AD=13,则四边形ABCD的面积为( )| A、72 | B、36 | C、66 | D、42 |
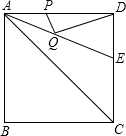 如图,正方形ABCD的边长是4,∠DAC的平分线交DC于点E,若点P、Q分别是AD和AE上的动点,则DQ+PQ的最小值( )
如图,正方形ABCD的边长是4,∠DAC的平分线交DC于点E,若点P、Q分别是AD和AE上的动点,则DQ+PQ的最小值( ) 16、如图,∠B=42°,∠A+10°=∠1,∠ACD=64°,则AB与CD的关系是
16、如图,∠B=42°,∠A+10°=∠1,∠ACD=64°,则AB与CD的关系是