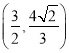题目内容
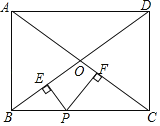
【题目】如图,矩形![]() 的顶点
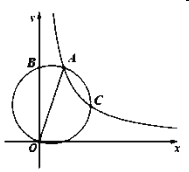
的顶点![]() 在反比例函数
在反比例函数![]() 的图象上,且
的图象上,且![]() ,
,![]() .若动点
.若动点![]() 从
从![]() 开始沿
开始沿![]() 向
向![]() 以每秒1个单位长度的速度运动,同时动点
以每秒1个单位长度的速度运动,同时动点![]() 从
从![]() 开始沿
开始沿![]() 向
向![]() 以每秒2个单位长度的速度运动,当其中一个动点到达端点时,另一个动点随之停止运动,设运动时间为
以每秒2个单位长度的速度运动,当其中一个动点到达端点时,另一个动点随之停止运动,设运动时间为![]() 秒.
秒.
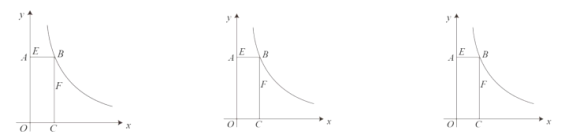
(1)求反比例函数的表达式;
(2)当![]() 时,在
时,在![]() 轴上存在点
轴上存在点![]() ,使
,使![]() 的周长最小,请求出此时点
的周长最小,请求出此时点![]() 的坐标,并直接写出
的坐标,并直接写出![]() 的周长最小值;
的周长最小值;
(3)在双曲线上是否存在一点![]() ,使以点
,使以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是平行四边形?若存在,请直接写出满足条件
为顶点的四边形是平行四边形?若存在,请直接写出满足条件![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1)![]() ;(2)点
;(2)点![]() 坐标为
坐标为![]() ,
,![]() ;(3)存在,
;(3)存在,![]() 或2
或2
【解析】
(1)通过AB,BC的长度,求出点B的坐标,将点B的坐标代入即可求出反比例函数的表达式;
(2)当![]() 时,可求出E,F的坐标,作E关于y轴的对称点E’,连接E’F,则E’F与y轴的交点即为所求的点D,然后再求
时,可求出E,F的坐标,作E关于y轴的对称点E’,连接E’F,则E’F与y轴的交点即为所求的点D,然后再求![]() 的周长的最小值即可;
的周长的最小值即可;
(3)分别用含t的代数式表示出E,F,B的坐标,分![]() 可以分别与
可以分别与![]() 、
、![]() 、
、![]() 相对三种情况,根据相对关系表达出
相对三种情况,根据相对关系表达出![]() 坐标,最后将
坐标,最后将![]() 坐标代入反比例函数解析式求解.
坐标代入反比例函数解析式求解.
(1)![]()
![]()
∵点B在反比例函数图像上,
![]()
![]()
![]()
(2)![]() 时,
时,![]() ,
, ![]() ,
,![]() ,
,
∴![]() ,
,![]() .
.
作点![]() 关于
关于![]() 轴得对称点
轴得对称点![]() ,连接
,连接![]() 交
交![]() 轴与一点,即为所求的点
轴与一点,即为所求的点![]() ,
,
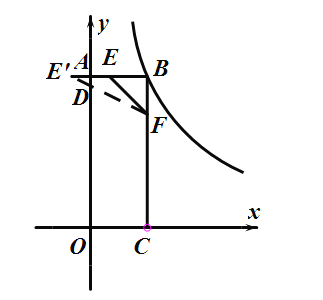
设直线![]() 解析式为
解析式为![]()
将点E’,F代入解析式中得![]() ,解得
,解得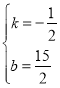 ,
,
∴直线![]() 解析式为
解析式为![]() ,
,
令![]() 得
得![]() ,
,
∴点![]() 坐标为
坐标为![]() ,
,
![]()
![]()
在![]() 中,由勾股定理得,
中,由勾股定理得,![]() ,
,
在![]() 中,由勾股定理得,
中,由勾股定理得,![]() ,
,
∴![]() ;
;
(3)存在,![]() 或2,
或2,

由题意得:![]() 、
、![]() 、
、![]() ,
,
①![]() 与
与![]() 相对时,此时M在F的右侧,
相对时,此时M在F的右侧,![]() ,
,
∵四边形BEFM是平行四边形,
![]() ,
,
![]() ,
,
∵点M在反比例函数上,
∴![]() ,解得
,解得![]() ,
,
由于![]() ,∴
,∴![]() ;
;
②![]() 与
与![]() 相对,此时M在E的正上方,
相对,此时M在E的正上方,![]() ,
,
∵四边形EFBM是平行四边形,
![]()
![]() ,
,
∵点M在反比例函数上,
∴![]() ,解得
,解得![]() 或2,
或2,
由于![]() ,∴
,∴![]() .
.
③![]() 与
与![]() 相对时,点M不在反比例函数图像上,所以此时不存在点M
相对时,点M不在反比例函数图像上,所以此时不存在点M
综上所述,![]() 或2
或2

 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案【题目】下表是某班同学随机投掷一枚硬币的试验结果( )
抛掷次数n | 50 | 100 | 150 | 200 | 250 | 300 | 350 | 400 | 450 | 500 |
“正面向上”次数m | 22 | 52 | 71 | 95 | 116 | 138 | 160 | 187 | 214 | 238 |
“正面向上”频率 | 0.44 | 0.52 | 0.47 | 0.48 | 0.46 | 0.46 | 0.46 | 0.47 | 0.48 | 0.48 |
下面有三个推断:
①表中没有出现“正面向上”的概率是0.5的情况,所以不能估计“正面向上”的概率是0.5;
②这些次试验投掷次数的最大值500,此时“正面向上”的频率是0.48,所以“正面向上”的概率是0.48;
③投掷硬币“正面向上”的概率应该是确定的,但是大量重复试验反映的规律并非在每一次试验中都发生;
其中合理的是( )
A. ①②B. ①③C. ③D. ②③