题目内容
已知
=-1,求(
)+
+
×(
)×
×
的值.
| abc |
| |abc| |
| a |
| |a| |
| |b| |
| b |
| c |
| |c| |
| ac |
| |bc| |
| bc |
| |ac| |
| ab |
| |ab| |
分析:由
=-1,可知,a、b、c的符号有两种可能的情况:①a、b、c全是负数;②a、b、c两正一负;由此分类探讨求得答案即可.
| abc |
| |abc| |
解答:解:
=-1,
①当a、b、c全是负数,
则原式=
+
+
×
═
+
+
=-1-1-1
=-3;
②a、b、c两正一负,
则原式=
+
+
×
=
+
+
,一定是两个1与一个-1的和,
计算的结果是1+1-1=1.
所以原式的值是1或-3.
| abc |
| |abc| |
①当a、b、c全是负数,
则原式=
| a |
| |a| |
| |b| |
| b |
| c |
| |c| |
| (abc)2 |
| |abc|2 |
═
| a |
| |a| |
| |b| |
| b |
| c |
| |c| |
=-1-1-1
=-3;
②a、b、c两正一负,
则原式=
| a |
| |a| |
| |b| |
| b |
| c |
| |c| |
| (abc)2 |
| |abc|2 |
=
| a |
| |a| |
| |b| |
| b |
| c |
| |c| |
计算的结果是1+1-1=1.
所以原式的值是1或-3.
点评:此题考查有理数的混合运算,和绝对值的意义,注意分类探讨得出答案.

练习册系列答案
相关题目
 如图:已知Rt△ABC中∠C=90°,AC=3,BC=4,点E在AC上,E与A、C均不重合.
如图:已知Rt△ABC中∠C=90°,AC=3,BC=4,点E在AC上,E与A、C均不重合.
 ∠ABC,∠3=
∠ABC,∠3=
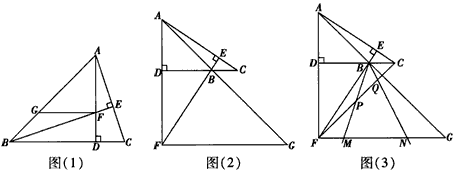
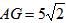 ,DC=3,将一个45°角的顶点与点B重合并绕点B旋转,这个角的两边分别交线段FG于M、N两点(如图(3)),连接CF,线段CF分别与线段BM、线段BN相交于P、Q两点,若
,DC=3,将一个45°角的顶点与点B重合并绕点B旋转,这个角的两边分别交线段FG于M、N两点(如图(3)),连接CF,线段CF分别与线段BM、线段BN相交于P、Q两点,若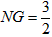 ,求线段PQ的长。
,求线段PQ的长。