题目内容
【题目】一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为![]() ,两车之间的距离为)
,两车之间的距离为)![]() ,图中的折线表示
,图中的折线表示![]() 与
与![]() 之间的函数关系,根据图象进行探究:
之间的函数关系,根据图象进行探究:
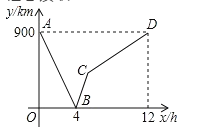
(1)甲、乙两地之间的距离为 ![]() ;
;
(2)请解释图中点![]() 的实际意义:__________;
的实际意义:__________;
(3)求线段![]() 所表示的
所表示的![]() 与
与![]() 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量![]() 的取值范围.
的取值范围.
【答案】(1)900;(2)当慢车行驶4h时,慢车和快车相遇;(3)![]()
【解析】
(1)根据图象的性质求解即可;
(2)根据图象的性质、数形结合的思想求解即可;
(3)设线段![]() 的函数关系式为
的函数关系式为![]() 将点
将点![]() 代入函数表达式中求出解析式即可.
代入函数表达式中求出解析式即可.
(1)![]()
(2)图中点![]() 的实际意义是:当慢车行驶
的实际意义是:当慢车行驶![]() 时,慢车和快车相遇
时,慢车和快车相遇
(3)设线段![]() 的函数关系式为
的函数关系式为![]()
由题意知:点![]() 表示快车到达乙地
表示快车到达乙地
易求出快车速度为![]() 、甲、乙两地距离为
、甲、乙两地距离为![]()
故此刻时间为![]() ,两车之间的距离为
,两车之间的距离为![]() ,
,
故![]()
将点![]() 代入函数表达式中得:
代入函数表达式中得: ![]()

练习册系列答案
相关题目
【题目】某校为了解七、八年级学生对“防溺水”安全知识的掌握情况,从七、八年级各随机抽取50名学生进行测试,并对成绩(百分制)进行整理、描述和分析.部分信息如下:
a.七年级成绩频数分布直方图:
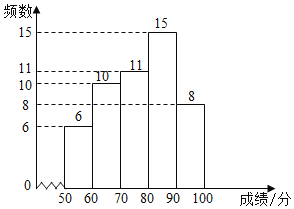
b.七年级成绩在![]() 这一组的是:70 72 74 75 76 76 77 77 77 78 79
这一组的是:70 72 74 75 76 76 77 77 77 78 79
c.七、八年级成绩的平均数、中位数如下:
年级 | 平均数 | 中位数 |
七 | 76.9 | m |
八 | 79.2 | 79.5 |
根据以上信息,回答下列问题:
(1)在这次测试中,七年级在80分以上(含80分)的有 人;
(2)表中m的值为 ;
(3)在这次测试中,七年级学生甲与八年级学生乙的成绩都是78分,请判断两位学生在各自年级的排名谁更靠前,并说明理由;
(4)该校七年级学生有400人,假设全部参加此次测试,请估计七年级成绩超过平均数76.9分的人数.