题目内容
【题目】如图所示，在平面直角坐标系中，四边形ABCD是直角梯形，BC∥AD，∠BAD=90°，BC与y轴相交于点M，且M是BC的中点，A，B，D三点的坐标分别是A（﹣1，0），B（﹣l，2），D（3，0）．连接DM，并把线段DM沿DA方向平移到ON．若抛物线y=ax2+bx+c经过点D，M，N．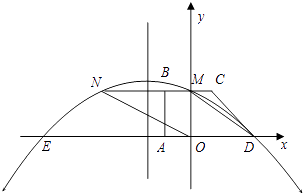
（1）求抛物线的解析式．
（2）抛物线上是否存在点P，使得PA=PC？若存在，求出点P的坐标；若不存在，请说明理由．
（3）设抛物线与x轴的另一个交点为E，点Q是抛物线的对称轴上的一个动点，当点Q在什么位置时有|QE﹣QC|最大？并求出最大值．
【答案】
（1）解：∵BC∥AD，B（﹣1，2），M是BC与y轴的交点，∴M（0，2），
∵DM∥ON，D（3，0），
∴N（﹣3，2），
则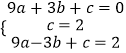 
，
解得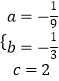 
，
∴y=﹣ 
x2﹣ 
x+2
（2）解：方法一：连接AC交y轴于G，
∵M是BC的中点，
∴AO=BM=MC，AB=BC=2，
∴AG=GC，即G（0，1），
∵∠ABC=90°，
∴BG⊥AC，即BG是AC的垂直平分线，要使PA=PC，即点P在AC的垂直平分线上，故P在直线BG上，
∴点P为直线BG与抛物线的交点，
设直线BG的解析式为y=kx+b，
则 
，
解得 
，
∴y=﹣x+1，
∴ 
，
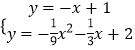解得 
， 
，
∴点P（3+3 
，﹣2﹣3 ）或P（3﹣3 ，﹣2+3 ）
方法二：∵M是BC的中点M（0，2），B（﹣1，2），
∴C（1，2），
设P（t，﹣ 
），A（﹣1，0），C（1，2），
∵PA=PC，
∴（t+1）2+（﹣ ）2=（t﹣1）2+（﹣ 
）2，
t2+2t+1+（﹣ ）2+4（﹣ ）+4=t2﹣2t+1+（﹣ ）2，
∴t2﹣6t﹣9=0，t1=3+3 ，t2=3﹣3 ，
∴P1（3+3 ，﹣2﹣3 ），P2（3﹣3 ，﹣2+3 ）
（3）解：方法一：∵y=﹣ x2﹣ x+2=﹣ （x+ 
）2+2 
，
∴对称轴x=﹣ ，
令﹣ x2﹣ x+2=0，
解得x1=3，x2=﹣6，
∴E（﹣6，0），
故E、D关于直线x=﹣ 对称，
∴QE=QD，
∴|QE﹣QC|=|QD﹣QC|，
要使|QE﹣QC|最大，则延长DC与x=﹣ 相交于点Q，即点Q为直线DC与直线x=﹣ 的交点，
由于M为BC的中点，
∴C（1，2），
设直线CD的解析式为y=kx+b，
则 
，
解得 
，
∴y=﹣x+3，
当x=﹣ 时，y= +3= 
，
故当Q在（﹣ ， ）的位置时，|QE﹣QC|最大，
过点C作CF⊥x轴，垂足为F，
则CD= 
= 
=2
方法二：∵y=﹣ 
，
∴对称轴x=﹣ ，
∵点E与点D关于x=﹣ 对称，
∴E（﹣6，0），QE=QD，
∴|QE﹣QC|=|QD﹣QC|，
要使|QE﹣QC|最大，延长DC与对称轴交于点Q，即点Q为直线DC与直线x=﹣ 的交点，
∵D（3，0），C（1，2），
∴lDC：y=﹣x+3，
当x=﹣ 时，y= ，
∴Q（﹣ ， ）．
∴CD= 
．
【解析】（1）由已知BC∥AD，DM∥ON得出四边形ODMN是平行四边形，OD=BM，根据B（﹣1，2），D（3，0）就可以求出点M、点D的坐标，用待定系数法就可以求出抛物线的解析式。
（2）方法一：连接AC交y轴于G，根据M是BC的中点求出点C的坐标，根据A、B、C三点坐标判断BG是AC的垂直平分线，再求出直线BG的解析式，与二次函数联立，解方程组，即可求出点P的坐标；方法二：M是BC的中点，设出点P的坐标，根据勾股定理表示出PA、PC的长，根据PA=PC，建立方程，求解即可求出点P的坐标。
（3）方法一、由抛物线的对称性可知QE=QD，当Q、C、D三点共线时|QE﹣QC|最大，再求出直线CD的函数解析式，再求出点Q的坐标，过点C作CF⊥x轴，垂足为F，此时|QE﹣QC|=CD，就可求出CD的长；方法二、找出点E关于抛物线对称轴的对称点D，连接DC与对称轴的交点即为点Q。
【考点精析】本题主要考查了公式法和确定一次函数的表达式的相关知识点，需要掌握要用公式解方程，首先化成一般式．调整系数随其后，使其成为最简比．确定参数abc，计算方程判别式．判别式值与零比，有无实根便得知．有实根可套公式，没有实根要告之；确定一个一次函数，需要确定一次函数定义式y=kx+b（k不等于0）中的常数k和b．解这类问题的一般方法是待定系数法才能正确解答此题．
