题目内容
已知a，b，c都是不为0的有理数，且满足|abc|=-abc，设M=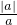
+
+
，则M所有可能的值为
- A.-3，-1，1，3
- B.-1，-3，1
- C.1，-3
- D.1，3
C
分析：由已知|abc|=-abc，根据绝对值的性质，则此题要分两种情况分析求值．
当a、b、c全为负数时；两个正数、一个负数时；2种情况．
解答：（1）当a、b、c全为负数时，
原式=-1-1-1=-3；
（2）当a、b、c中两个正数、一个负数时，
原式=-1+1+1=1；
所以M所有可能的值为1，-3．
故选：C．
点评：主要考查绝对值性质的运用．此题没有关于a，b，c的正负说明，所以要分情况讨论．
分析：由已知|abc|=-abc，根据绝对值的性质，则此题要分两种情况分析求值．
当a、b、c全为负数时；两个正数、一个负数时；2种情况．
解答：（1）当a、b、c全为负数时，
原式=-1-1-1=-3；
（2）当a、b、c中两个正数、一个负数时，
原式=-1+1+1=1；
所以M所有可能的值为1，-3．
故选：C．
点评：主要考查绝对值性质的运用．此题没有关于a，b，c的正负说明，所以要分情况讨论．
练习册系列答案
阅读快车系列答案
相关题目
的所有可能的值.