题目内容
若x是自然数，设y=x4+2x3+2x2+2x+1，则（ ）
| A．y一定是完全平方数 |
| B．存在有限个，使y是完全平方数 |
| C．y一定不是完全平方数 |
| D．存在无限多个，使y是完全平方数 |
当x=0时，y=1．y是完全平方数．
当x为大于0的自然数时．x4+2x3+2x2＜y＜x4+x2+1+2x3+2x2+2x．
故（x2+x）2＜y＜（x2+x+1）2．y一定不是完全平方数．
故存在有限个，使y是完全平方数．
故选B．
当x为大于0的自然数时．x4+2x3+2x2＜y＜x4+x2+1+2x3+2x2+2x．
故（x2+x）2＜y＜（x2+x+1）2．y一定不是完全平方数．
故存在有限个，使y是完全平方数．
故选B．
练习册系列答案
阅读快车系列答案
相关题目
设a、b是自然数，且其中一个是奇数，若ax=by=20082，且
+
=
，则2a+b的一切可能的取值是（ ）
| 1 |
| x |
| 1 |
| y |
| 1 |
| z |
| A、2010，510 |
| B、267，4017 |
| C、2010，510，267，4017 |
| D、2008，2006，2004，2002 |
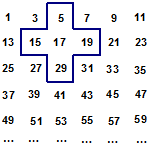将连续的奇数1，3，5，7，…，排成如图所示的数表，用十字框任意框出5个数．