题目内容
如图,AB是⊙O的直径,C是弧AB的中点,D是⊙O的切线CN上一点,BD交AC于点E,且BA= BD.
(1)求证:∠ACD=45°;
(2)若OB=2,求DC的长.

 (1)证明:∵C是弧AB的中点,
(1)证明:∵C是弧AB的中点,
∴弧AC=弧BC,
∴AC=BC,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠BAC=∠CBA=45°,
连接OC,∵OC=OA,
∴∠AC0=45°,
∵CN是⊙O切线,
∴∠OCD=90°,
∴∠ACD= 45°.………………5分
45°.………………5分
(2)解:作BH⊥DC于H点,
∵∠ACD=45°,
∴∠DCB=135°,
∴∠BCH=45°,
∵OB=2,
∴BA=BD=4,AC=BC=2 .
.
∵BC=2 ,
,
∴BH=CH=2,
设DC=x,在Rt△DBH中,
利用勾股定理:(x+2)2+22=42,
解得:x=−2±2 (舍负的),
(舍负的),
∴x=−2+2 ,
,
∴DC的长为:−2+2 .………………10分
.………………10分

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
观察下列一组图形中点的个数,其中第1个图中共有4个点,第2个图中共有10个点,第3个图中共有19个点,……;按此规律第5个图中共有点的个数是
|
第1个图 第2个图 第3个图
A. 31 B. 46 C. 51 D. 66
 ,上、下边衬等宽,左、右边衬等宽,应如何设计四周边衬的宽度(结果保留小数点后一位,参考数据:
,上、下边衬等宽,左、右边衬等宽,应如何设计四周边衬的宽度(结果保留小数点后一位,参考数据: ≈2.236).
≈2.236).

 轴交于点
轴交于点 (1,0)和点
(1,0)和点 ,与
,与 轴交于点
轴交于点 (0,6),对称轴为直线
(0,6),对称轴为直线 ,求二次函数的解析式并写出图像最低点的坐标.
,求二次函数的解析式并写出图像最低点的坐标.
 的根是
的根是 B.
B.
 D.
D.
 中,直线
中,直线 经过
经过 、
、 ,
, 的半径为2(
的半径为2( 为坐标原点),点
为坐标原点),点 是直线
是直线 ,
,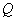 为切点,则切线长
为切点,则切线长
 B.3 C.
B.3 C. D.
D.
 与
与 于点
于点 ,
, ,
,
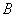 ,
, 的延长线交直线
的延长线交直线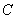 .
. 的数量关系,并说明理由;
的数量关系,并说明理由;
 ,求
,求 的长.
的长. 