题目内容
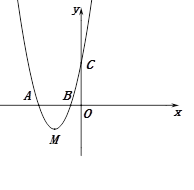
【题目】如图,抛物线经过A(![]() ),B(
),B(![]() ),C(
),C(![]() )三点.
)三点.
(1)求抛物线的解析式;
(2)在直线AC下方的抛物线上有一点D,使得△DCA的面积最大,求点D的坐标;
(3)设点M是抛物线的顶点,试判断抛物线上是否存在点H满足![]() ?若存在,请求出点H的坐标;若不存在,请说明理由.
?若存在,请求出点H的坐标;若不存在,请说明理由.
【答案】(1)抛物线的解析式为![]() ;
;
(2)点D的坐标为(-1,-1).
(3)点H存在.点H坐标为![]() .
.
【解析】
试题(1)由待定系数法即可得;
由题意可求得直线AC的解析式为![]() .如图,
.如图,
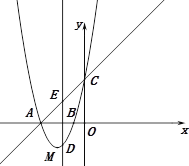
设D点的横坐标为t(-2<t<0),则D点的纵坐标为![]() .过D作y轴的平行线交AC于E.则E点的坐标为
.过D作y轴的平行线交AC于E.则E点的坐标为![]() .从而可得
.从而可得![]()
![]() ,用h表示点C到线段DE所在直线的距离,则可得
,用h表示点C到线段DE所在直线的距离,则可得![]()
![]() ,由-2<t<0可知当t=-1时,△DAC面积最大,此时点D的坐标为(-1,-1).
,由-2<t<0可知当t=-1时,△DAC面积最大,此时点D的坐标为(-1,-1).
点H存在.
由(1)知,点M的坐标为![]()
如图,假设存在点H,满足![]()
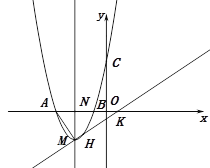
作直线MH交![]() 轴于点K(
轴于点K(![]() ,0),作MN⊥
,0),作MN⊥![]() 轴于点N. 可得
轴于点N. 可得![]() ,从而有
,从而有![]() ,从而得点K的坐标为(
,从而得点K的坐标为(![]() ),得直线MK的解析式为
),得直线MK的解析式为![]() ,解方程组
,解方程组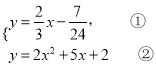 ,得
,得![]() ,
,![]() .将
.将![]() 代入
代入![]() 中,解得
中,解得![]() ,由于直线MN与抛物线有两个交点(其中一点为顶点M).从而知 抛物线上必存在一点H,使∠AMH=90, 此时点H坐标为
,由于直线MN与抛物线有两个交点(其中一点为顶点M).从而知 抛物线上必存在一点H,使∠AMH=90, 此时点H坐标为![]() .
.
试题解析:(1)∵该抛物线过点C(0,2),∴可设该抛物线的解析式为![]() .
.
将A(-2,0),B(-![]() ,0)代入,得
,0)代入,得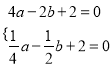 ,解得:
,解得:![]()
∴此抛物线的解析式为![]() ;
;
(2)由题意可求得直线AC的解析式为![]() .如图,
.如图,

设D点的横坐标为t(-2<t<0),则D点的纵坐标为![]() .
.
过D作y轴的平行线交AC于E.∴E点的坐标为![]() .
.
∴![]()
![]() ,用h表示点C到线段DE所在直线的距离,
,用h表示点C到线段DE所在直线的距离,
∴![]()
![]()
∵-2<t<0
∴当t=-1时,△DAC面积最大,此时点D的坐标为(-1,-1).
(3)点H存在.
由(1)知,点M的坐标为![]()
如图,假设存在点H,满足![]()
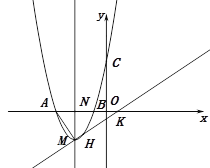
作直线MH交![]() 轴于点K(
轴于点K(![]() ,0),作MN⊥
,0),作MN⊥![]() 轴于点N.
轴于点N.
∵![]() ,
,![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,∴
,∴![]() ,∴
,∴![]()
∴![]() ,∴
,∴![]() ,∴点K的坐标为(
,∴点K的坐标为(![]() ),所以直线MK的解析式为
),所以直线MK的解析式为![]() ,∴
,∴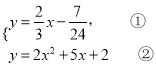 ,把①代入②,化简,得:
,把①代入②,化简,得:![]() ,
,![]() >0.
>0.
∴![]() ,
,![]() .将
.将![]() 代入
代入![]() 中,解得
中,解得![]()
∴ 直线MN与抛物线有两个交点(其中一点为顶点M).
∴ 抛物线上必存在一点H,使∠AMH=90, 此时点H坐标为![]() .
.

 名校课堂系列答案
名校课堂系列答案