Question

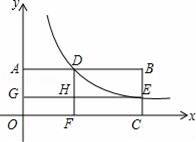
如图，矩形OABC的顶点A在y轴上，C在x轴上，双曲线y=与AB交于点D，与BC交于点E，DF⊥x轴于点F，EG⊥y轴于点G，交DF于点H．若矩形OGHF和矩形HDBE的面积分别是1和2，则k的值为（　　）

A．    B． +1     C．      D．2

　

Answer 1

B【考点】反比例函数系数k的几何意义．

【专题】计算题．

【分析】设D（t，），由矩形OGHF的面积为1得到HF=，于是根据反比例函数图象上点的坐标特征可表示出E点坐标为（kt，），接着利用矩形面积公式得到（kt﹣t）•（﹣）=2，然后解关于k的方程即可得到满足条件的k的值．

【解答】解：设D（t，），

∵矩形OGHF的面积为1，DF⊥x轴于点F，

∴HF=，

而EG⊥y轴于点G，

∴E点的纵坐标为，

当y=时， =，解得x=kt，

∴E（kt，），

∵矩形HDBE的面积为2，

∴（kt﹣t）•（﹣）=2，

整理得（k﹣1）²=2，

而k＞0，

∴k=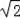+1．

故选B．

【点评】本题考查了反比例函数比例系数k的几何意义：在反比例函数y=图象中任取一点，过这一个点向x轴和y轴分别作垂线，与坐标轴围成的矩形的面积是定值|k|．