题目内容
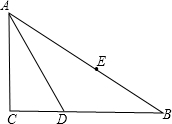 如图,△ABC的三边长分别为AC=9,AB=15,BC=12,若将△ABC沿线段AB折叠,点C正好落在AB边上的点E处,求:
如图,△ABC的三边长分别为AC=9,AB=15,BC=12,若将△ABC沿线段AB折叠,点C正好落在AB边上的点E处,求:(1)△ACD面积;
(2)△ACD的周长.
分析:(1)设CD=x,则根据折叠的性质可得出AE=AC=9,EB=6,BD=12-x,在RT△CDB中可求出x的值,继而可得出△ACD面积.
(2)在RT△ACD中求出AD,继而可得出周长.
(2)在RT△ACD中求出AD,继而可得出周长.
解答: 解:(1)设CD=x,则根据折叠的性质可得出AE=AC=9,EB=6,BD=12-x,
解:(1)设CD=x,则根据折叠的性质可得出AE=AC=9,EB=6,BD=12-x,
在RT△CEB中,DE2+EB2=DB2,即x2+62=(12-x)2,
解得:x=
,即CD=
,
所以S△ACD=
×
×9=
;
(2)在RT△ACD中,AD=
=
,
所以△ACD的周长为:9+
+
=
.
 解:(1)设CD=x,则根据折叠的性质可得出AE=AC=9,EB=6,BD=12-x,
解:(1)设CD=x,则根据折叠的性质可得出AE=AC=9,EB=6,BD=12-x,在RT△CEB中,DE2+EB2=DB2,即x2+62=(12-x)2,
解得:x=
| 9 |
| 2 |
| 9 |
| 2 |
所以S△ACD=
| 1 |
| 2 |
| 9 |
| 2 |
| 81 |
| 4 |
(2)在RT△ACD中,AD=
| AC2+CD2 |
9
| ||
| 4 |
所以△ACD的周长为:9+
| 9 |
| 2 |
9
| ||
| 4 |
54+9
| ||
| 4 |
点评:此题考查了翻折变换及勾股定理的知识,解答本题的关键是求出CD的长度,继而两问均可求出来,难度一般.

练习册系列答案
相关题目
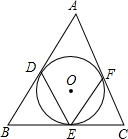 如图,△ABC的三边分别切⊙O于D,E,F,若∠A=40°,则∠DEF=
如图,△ABC的三边分别切⊙O于D,E,F,若∠A=40°,则∠DEF=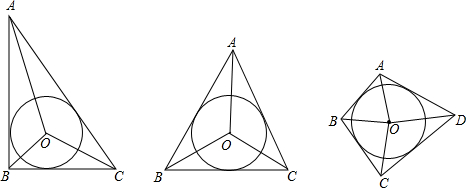
 如图,△ABC的三边AB、BC、AC的长分别为4,6,8,其三条角平分线将△ABC分成三个三角形,则S△OAB:S△OBC:S△OAC=
如图,△ABC的三边AB、BC、AC的长分别为4,6,8,其三条角平分线将△ABC分成三个三角形,则S△OAB:S△OBC:S△OAC= 如图,△ABC的三边长分别为AC=12,AB=15,BC=9.若将△ABC沿线段AD折叠,点C正好落在AB边上的点E处.求线段CD的长度.
如图,△ABC的三边长分别为AC=12,AB=15,BC=9.若将△ABC沿线段AD折叠,点C正好落在AB边上的点E处.求线段CD的长度.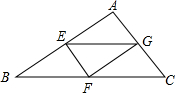 如图,△ABC的三边长分别是6cm、8cm、10cm,现在分别取三边的中点E、F、G,顺次连接E、F、G,则△EFG的面积为
如图,△ABC的三边长分别是6cm、8cm、10cm,现在分别取三边的中点E、F、G,顺次连接E、F、G,则△EFG的面积为