题目内容
一次函数y=kx+b的图象与x轴、y轴分别交于点A（2，0）、B（0，4）。
（1）求该函数的解析式；
（2）O为坐标原点，设OA、AB的中点分别为C、D，P为OB上一动点，求PC+PD的最小值，并求取得最小值时P点坐标。
（1）求该函数的解析式；
（2）O为坐标原点，设OA、AB的中点分别为C、D，P为OB上一动点，求PC+PD的最小值，并求取得最小值时P点坐标。
解：（1）将点A、B的坐标代人y=kx+b并计算得k=-2，b=4，
∴该函数的解析式为：y=-2x+4；
（2）设点C关于点O的对称点为C′，连接PC′、DC′，则PC=PC′，
∴PC+PD=PC′+ PD≥C′D，即C′、P、D共线时，PC+PD取得最小值是C′D，连接CD，
在Rt△DCC′中，
易得点P的坐标为（0，1），
∴该函数的解析式为：y=-2x+4；
（2）设点C关于点O的对称点为C′，连接PC′、DC′，则PC=PC′，
∴PC+PD=PC′+ PD≥C′D，即C′、P、D共线时，PC+PD取得最小值是C′D，连接CD，
在Rt△DCC′中，
易得点P的坐标为（0，1），
练习册系列答案
相关题目
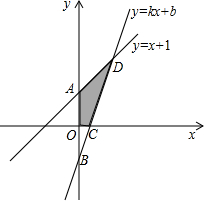x轴以及y=x+1的图象分别交于点C、D．
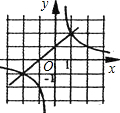一次函数y=kx+b与反比例函数y=
（2013•潍坊）如图，抛物线y=ax2+bx+c关于直线x=1对称，与坐标轴交与A，B，C三点，且AB=4，点D（2，