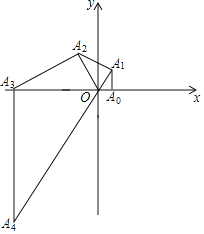
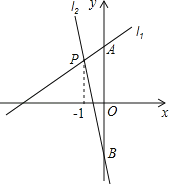
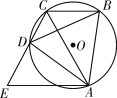
��Ŀ����
����Ŀ����ͼ����ֱ֪��![]() ��x�ᡢy��ֱ��ڵ�A����F�����뷴��������
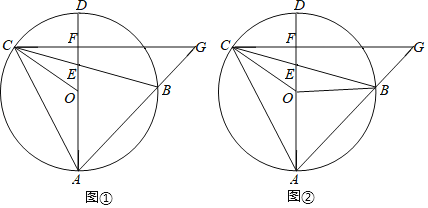
��x�ᡢy��ֱ��ڵ�A����F�����뷴��������![]() ��ͼ����B��C���㣨��B�ڵ�C����ࣩ����OAΪֱ������Բ��Բ��ΪP������B��x��Ĵ��ߣ�����ΪE�������ԲP���ڵ�D��
��ͼ����B��C���㣨��B�ڵ�C����ࣩ����OAΪֱ������Բ��Բ��ΪP������B��x��Ĵ��ߣ�����ΪE�������ԲP���ڵ�D��
��1����B��C�ĺ�����ֱ�Ϊx1��x2����x2x15����m��ֵ��
��2���ж��߶�DE�ij��Ƿ���m�ĸı���ı䣬������m�ĸı���ı䣬�����DE�ij�������m�ĸı���ı䣬��˵�����ɣ�
��3���ǵ�C����ֱ��DE�ĶԳƵ�ΪC�������ı���CDC��EΪ����ʱ��ֱ��д��C�������m��ֵ��

���𰸡���1��![]() ����2�����ı䣬
����2�����ı䣬![]() ����3��
����3��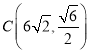 ��
��![]()
��������
��1����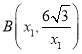 ��
��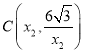 �����ݵ�B����C��һ�κ����뷴����������ͼ���ϣ��г������飬��⼴�ɣ�
�����ݵ�B����C��һ�κ����뷴����������ͼ���ϣ��г������飬��⼴�ɣ�
��2������![]() ��
��![]() ������
������![]() �ó�
�ó�![]() ����
����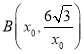 ��
��![]() ��ͨ������ó�
��ͨ������ó�![]() ��
��![]() ��������⼴�ɣ�
��������⼴�ɣ�
��3������CC������DE��CC������G���ɣ�2�������ε����ʵó�DG��EG��![]() �������ó���C�������꣬��⼴�ɣ�
�������ó���C�������꣬��⼴�ɣ�
�⣺��1��������ã�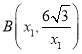 ��
��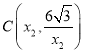
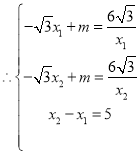 ��
��
��ȥ![]() �ã�
�ã�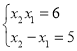 ��
��
��ã�![]() ����ȥ����1��
����ȥ����1��![]() ��
��
���![]() ������
������![]() �ã�
�ã�![]() ��
��
��2������![]() ��
��![]() ����֤
����֤![]() ��
��
��![]() ��
��![]() ��
��
��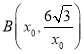 ����
���� ����
����![]() ��
��
![]() ��
��![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
��DE�ij����ı䣬Ϊ![]() ��
��
��3������CC������DE��CC������G��
�ɣ�2���ã�![]() ��
��
���ı���CDC��EΪ���Σ�
��DG��EG��![]() ��
��
��C��������Ϊ![]() ��
��
��y��![]() ʱ��
ʱ��![]() ��
��
��![]() ��
��
��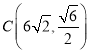 ��
��
����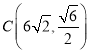 ����
����![]() �еã�
�еã�![]() ��
��
��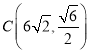 ��
��![]() ��
��