题目内容
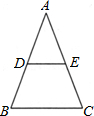 如图,△ABC中,BC=2,DE是它的中位线,下面三个结论:(1)DE=1;(2)△ADE∽△ABC;(3)△ADE的面积与△ABC的面积之比为1:4.其中正确的有( )
如图,△ABC中,BC=2,DE是它的中位线,下面三个结论:(1)DE=1;(2)△ADE∽△ABC;(3)△ADE的面积与△ABC的面积之比为1:4.其中正确的有( )| A、0个 | B、1个 | C、2个 | D、3个 |
分析:本题需先根据相似三角形的判定和性质以及三角形的中位线的性质逐个分析,即可得出正确答案.
解答:解:(1)∵△ABC中,BC=2,DE是它的中位线,
∴DE=
BC
=
×2
=1
故本选项正确;
(2)∵△ABC中,DE是它的中位线
∴DE∥BC
∴△ADE∽△ABC
故本选项正确;
(3)∵△ADE∽△ABC,相似比为1:2
∴△ADE的面积与△ABC的面积之比为1:4.
故本选项正确
故选D.
∴DE=
| 1 |
| 2 |
=
| 1 |
| 2 |
=1
故本选项正确;
(2)∵△ABC中,DE是它的中位线
∴DE∥BC
∴△ADE∽△ABC
故本选项正确;
(3)∵△ADE∽△ABC,相似比为1:2
∴△ADE的面积与△ABC的面积之比为1:4.
故本选项正确
故选D.
点评:本题主要考查了相似三角形的判定和性质,在解题时要注意与三角形的中位线的性质相结合是本题的关键.

练习册系列答案
相关题目
 26、已知:如图,△ABC中,点D在AC的延长线上,CE是∠DCB的角平分线,且CE∥AB.
26、已知:如图,△ABC中,点D在AC的延长线上,CE是∠DCB的角平分线,且CE∥AB. 27、已知:如图,△ABC中,∠BAC=60°,D、E两点在直线BC上,连接AD、AE.
27、已知:如图,△ABC中,∠BAC=60°,D、E两点在直线BC上,连接AD、AE. 27、如图,△ABC中,AD⊥BC于D,DN⊥AC于N,DM⊥AB于M
27、如图,△ABC中,AD⊥BC于D,DN⊥AC于N,DM⊥AB于M 14、如图,△ABC中,∠BAC=120°,AD⊥BC于D,且AB+BD=DC,则∠C的大小是( )
14、如图,△ABC中,∠BAC=120°,AD⊥BC于D,且AB+BD=DC,则∠C的大小是( ) 已知,如图,△ABC中,点D在BC上,且∠1=∠C,∠2=2∠3,∠BAC=70°.
已知,如图,△ABC中,点D在BC上,且∠1=∠C,∠2=2∠3,∠BAC=70°.