题目内容
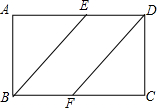 如图所示,在正方形ABCD中,点E、F分别是AD、BC的中点.求证:四边形BFDE是平行四边形.
如图所示,在正方形ABCD中,点E、F分别是AD、BC的中点.求证:四边形BFDE是平行四边形.
证明:∵四边形ABCD是正方形,
∴AD=BC,AD∥BC,即DE∥BF,
∵点E、F是AD、BC的中点,
∴DE= AD,BF=
AD,BF= BC,
BC,
∴DE=BF,又DE∥BF
∴四边形BFDE是平行四边形.
分析:在正方形ABCD中,点E、F分别是AD、BC的中点,再加上一组对边平行,即可证明其是平行四边形.
点评:掌握正方形的性质及平行四边形的判定定理.
∴AD=BC,AD∥BC,即DE∥BF,
∵点E、F是AD、BC的中点,
∴DE=
 AD,BF=
AD,BF= BC,
BC,∴DE=BF,又DE∥BF
∴四边形BFDE是平行四边形.
分析:在正方形ABCD中,点E、F分别是AD、BC的中点,再加上一组对边平行,即可证明其是平行四边形.
点评:掌握正方形的性质及平行四边形的判定定理.

练习册系列答案
相关题目
 如图所示,在正方形ABCD中,DE=EC,AD=4FD,则tan∠FBE=
如图所示,在正方形ABCD中,DE=EC,AD=4FD,则tan∠FBE= (2013•凤阳县模拟)如图所示,在正方形ABCD的对角线上取点E,使得∠BAE=15°,连结AE,CE.延长CE到F,连结BF,使得BC=BF.若AB=1,则下列结论:①AE=CE;②F到BC的距离为
(2013•凤阳县模拟)如图所示,在正方形ABCD的对角线上取点E,使得∠BAE=15°,连结AE,CE.延长CE到F,连结BF,使得BC=BF.若AB=1,则下列结论:①AE=CE;②F到BC的距离为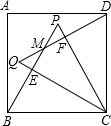 如图所示,在正方形ABCD中,△PCB和△QCD是正三角形,BP与QD相交于M,QC与PB相交于F,请你猜想QM与PM的大小关系?并证明你的猜想.
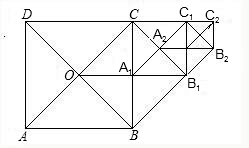
如图所示,在正方形ABCD中,△PCB和△QCD是正三角形,BP与QD相交于M,QC与PB相交于F,请你猜想QM与PM的大小关系?并证明你的猜想. 如图所示,在正方形网格上有一个△ABC.
如图所示,在正方形网格上有一个△ABC.