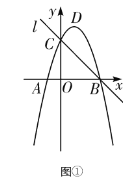
ĢāÄæÄŚČŻ
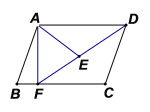
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ![]() ÖŠ£¬
ÖŠ£¬![]() £®µć
£®µć![]() “Óµć
“Óµć![]() ³ö·¢£¬ŃŲ
³ö·¢£¬ŃŲ![]() ·½ĻņŅŌĆæĆė
·½ĻņŅŌĆæĆė![]() øöµ„Ī»³¤¶ČµÄĖŁ¶ČĻņÖÕµć
øöµ„Ī»³¤¶ČµÄĖŁ¶ČĻņÖÕµć![]() ŌĖ¶Æ£Øµć
ŌĖ¶Æ£Øµć![]() ²»Óė
²»Óė![]() ÖŲŗĻ£©£¬¹żµć
ÖŲŗĻ£©£¬¹żµć![]() ×÷
×÷![]() ½»ÕŪĻß
½»ÕŪĻß![]() ÓŚµć
ÓŚµć![]() ŅŌ
ŅŌ![]() ĪŖ±ßĪŹĻĀ×÷Õż·½ŠĪ
ĪŖ±ßĪŹĻĀ×÷Õż·½ŠĪ![]() µć
µć![]() ĀäŌŚ±ß
ĀäŌŚ±ß![]() ÉĻÉčµć
ÉĻÉčµć![]() ŌĖ¶ÆµÄŹ±¼äĪŖ
ŌĖ¶ÆµÄŹ±¼äĪŖ![]() £ØĆė£©£®
£ØĆė£©£®

£Ø1£©Ö±½ÓÓĆŗ¬![]() µÄ“śŹżŹ½±ķŹ¾Ļ߶Ī
µÄ“śŹżŹ½±ķŹ¾Ļ߶Ī![]() µÄ³¤£®
µÄ³¤£®
£Ø2£©µ±µć![]() ĀäŌŚ±ß
ĀäŌŚ±ß![]() ÉĻŹ±£¬Ēó
ÉĻŹ±£¬Ēó![]() µÄÖµ£®
µÄÖµ£®
£Ø3£©µ±Õż·½ŠĪ![]() Óė
Óė![]() ÖŲµž²æ·ÖĶ¼ŠĪĪŖĖıߊĪŹ±£¬ÉčĖıߊĪµÄĆ껿ĪŖ
ÖŲµž²æ·ÖĶ¼ŠĪĪŖĖıߊĪŹ±£¬ÉčĖıߊĪµÄĆ껿ĪŖ![]() £ØĘ½·½µ„Ī»£©£¬Ēó
£ØĘ½·½µ„Ī»£©£¬Ēó![]() Óė
Óė![]() Ö®¼äµÄŗÆŹż¹ŲĻµŹ½£®
Ö®¼äµÄŗÆŹż¹ŲĻµŹ½£®
£Ø4£©µć![]() ĪŖ±ß
ĪŖ±ß![]() µÄÖŠµć£¬Ö±½ÓŠ“³öÖ±Ļß
µÄÖŠµć£¬Ö±½ÓŠ“³öÖ±Ļß![]() ½«Õż·½ŠĪ
½«Õż·½ŠĪ![]() ·Ö³ÉµÄĮ½²æ·ÖĶ¼ŠĪµÄĆ껿±ČĪŖ
·Ö³ÉµÄĮ½²æ·ÖĶ¼ŠĪµÄĆ껿±ČĪŖ![]() Ź±
Ź±![]() µÄÖµ£®
µÄÖµ£®
”¾“š°ø”æ£Ø1£©µ±![]() Ź±£¬
Ź±£¬![]() £®µ±
£®µ±![]() Ź±£¬
Ź±£¬![]() £»£Ø2£©
£»£Ø2£©![]() £»£Ø3£©µ±
£»£Ø3£©µ±![]() Ź±£®
Ź±£®![]() £»µ±
£»µ±![]() Ź±£®
Ź±£®![]() £»£Ø4£©
£»£Ø4£©![]() »ņ
»ņ![]()
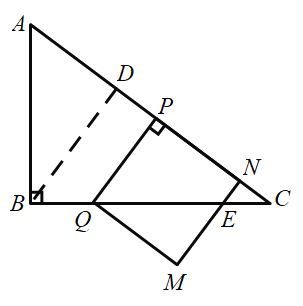
”¾½āĪö”æ
£Ø1£©Šč·ÖµćQŌŚABÉĻŗĶBCÉĻĮ½ÖÖĒéæö£¬½įŗĻČń½ĒČż½ĒŗÆŹż¼“æÉĒóµĆ¶ŌÓ¦µÄAPµÄ³¤£»
£Ø2£©±ķŹ¾³öAP£¬PN£¬NC£¬ÓĆAB=AP+PN+NC£¬¼“æÉĒó³ö£»
£Ø3£©ÓÉ£Ø2£©ÖŖ£¬Šč·ÖĪŖ![]() »ņ
»ņ![]() Į½²æ·ÖĢÖĀŪ£»
Į½²æ·ÖĢÖĀŪ£»
£Ø4£©ÓÉPF·ÖÕż·½ŠĪĆ껿ĪŖ1:2µÄĮ½²æ·Ö£¬µĆ³ö±ČĄż¹ŲĻµ£¬Ź¹ÓĆĘ½ŠŠĻß·ÖĻ߶Ī³É±ČĄż£¬¼ĘĖć½į¹ū£®
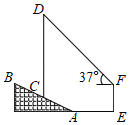
£Ø1£©×÷![]() £¬“¹×ćĪŖD
£¬“¹×ćĪŖD
”ß![]() £¬BC=4£¬AB=3£¬
£¬BC=4£¬AB=3£¬
”ąAC=5
ӧ![]()
”ą![]()
”ą![]()
”ą![]()
µćQŌŚABÉĻŹ±£¬ČēĶ¼ĖłŹ¾
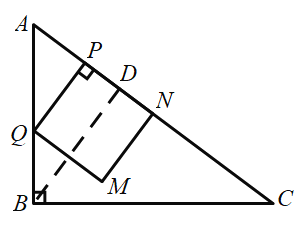
ŌŚ![]() ÖŠ£¬BC=4£¬AB=3£¬
ÖŠ£¬BC=4£¬AB=3£¬![]() £¬
£¬
ŌŚ![]() ÖŠ£¬
ÖŠ£¬![]() £¬Ōņ
£¬Ōņ![]() £Ø
£Ø![]() £©
£©
µ±µćQŌŚBCÉĻŹ±£¬ČēĶ¼ĖłŹ¾£ŗ
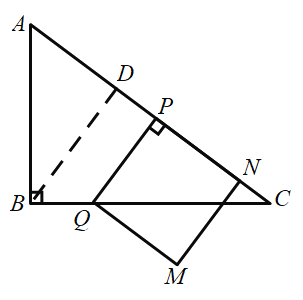
ŌŚ![]() ÖŠ£¬BC=4£¬AB=3£¬
ÖŠ£¬BC=4£¬AB=3£¬![]() £¬
£¬
ŌŚ![]() ÖŠ£¬
ÖŠ£¬![]() £¬Ōņ
£¬Ōņ![]() £Ø
£Ø![]() £©
£©
×ŪÉĻ£ŗµ±![]() Ź±£¬
Ź±£¬![]() £®µ±
£®µ±![]() Ź±£¬
Ź±£¬![]()
£Ø²»Š“Ȕֵ·¶Ī§²»æŪ·Ö£©
£Ø2£©µ±µć![]() ĀäŌŚ±ß
ĀäŌŚ±ß![]() ÉĻŹ±£¬ČēĶ¼ĖłŹ¾
ÉĻŹ±£¬ČēĶ¼ĖłŹ¾
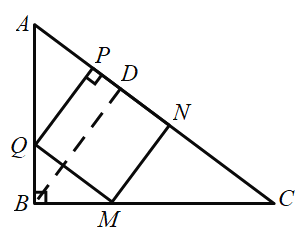
ÓÉ£Ø1£©ÖŖ£¬![]() £¬
£¬![]()
ŌŚ![]() ÖŠ£¬
ÖŠ£¬![]()
”ąAB=AP+PN+NC=![]() ½āµĆ
½āµĆ![]()
£Ø3£©ÓÉ£Ø2£©ÖŖ£¬Õż·½ŠĪ![]() Óė
Óė![]() ÖŲµž²æ·ÖĶ¼ŠĪĪŖĖıߊĪŹ±
ÖŲµž²æ·ÖĶ¼ŠĪĪŖĖıߊĪŹ±
![]() µÄȔֵ·¶Ī§ŹĒ£ŗ
µÄȔֵ·¶Ī§ŹĒ£ŗ![]() »ņ
»ņ![]()
µ±![]() Ź±£®“ĖŹ±ÖŲŗĻ²æ·ÖĪŖÕż·½ŠĪPQMNÕūĢ壬Ōņ
Ź±£®“ĖŹ±ÖŲŗĻ²æ·ÖĪŖÕż·½ŠĪPQMNÕūĢ壬Ōņ![]()
µ±![]() Ź±£®ČēĶ¼ĖłŹ¾£ŗ
Ź±£®ČēĶ¼ĖłŹ¾£ŗ
”ą![]() £¬
£¬![]()
ŌŚ![]() ÖŠ£¬
ÖŠ£¬![]()
”ą![]()
£Ø4£©µ±![]() Ź±£¬ČēĶ¼ĖłŹ¾£ŗ
Ź±£¬ČēĶ¼ĖłŹ¾£ŗ

“ĖŹ±![]()
Ö±ĻßPF½«Õż·½ŠĪPQMN·Ö³É1:2µÄĮ½²æ·Ö£¬¼“![]()
”ą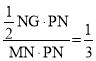 ¼“
¼“![]() £¬
£¬
”ą![]()
ŌŚ![]() ÖŠ£¬
ÖŠ£¬![]() £¬
£¬
”ą![]()
×÷![]() £¬“¹×ćĪŖH£¬
£¬“¹×ćĪŖH£¬
Ōņ![]()
ÓÖ![]()
”ą![]()
”ą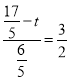 £¬½āµĆ
£¬½āµĆ![]()
µ±![]() Ź±£¬ČēĶ¼ĖłŹ¾£ŗ
Ź±£¬ČēĶ¼ĖłŹ¾£ŗ

Ķ¬ÉĻæÉÖŖ£ŗ![]()
ÓÉ![]() £¬µĆ
£¬µĆ![]()
ÓÖ![]()
”ą![]() £¬¼“
£¬¼“![]()
ÓÖFĪŖBCÖŠµć
”ą![]() ¼“
¼“![]()
”ą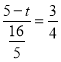 £¬½āµĆ
£¬½āµĆ![]()
×ŪÉĻ£ŗ![]() »ņ
»ņ![]() £®
£®

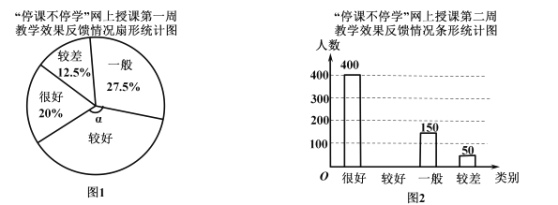
”¾ĢāÄæ”æÄ³Ń§Š£ĪŖĮĖĮĖ½ā¾ÅÄź¼¶Ń§ÉśÉĻѧʌ¼äĘ½¾łĆæĢģµÄĖÆĆßĒéæö£¬ĻÖ“ÓČ«Š£![]() Ćū¾ÅÄź¼¶Ń§ÉśÖŠĖ껜³éČ”ĮĖ²æ·Öѧɜ£¬µ÷²éĮĖÕāŠ©Ķ¬Ń§ÉĻѧʌ¼äĘ½¾łĆæĢģµÄĖÆĆߏ±¼ä
Ćū¾ÅÄź¼¶Ń§ÉśÖŠĖ껜³éČ”ĮĖ²æ·Öѧɜ£¬µ÷²éĮĖÕāŠ©Ķ¬Ń§ÉĻѧʌ¼äĘ½¾łĆæĢģµÄĖÆĆߏ±¼ä![]() £Øµ„Ī»£ŗŠ”Ź±£©£¬²¢øł¾Żµ÷²é½į¹ūĮŠ³öĶ³¼Ę±ķ£¬»ęÖĘ³ÉÉČŠĪĶ³¼ĘĶ¼£¬ČēĶ¼ĖłŹ¾£®ĒėÄćøł¾ŻĶ¼±ķĢį¹©µÄŠÅĻ¢½ā“šĻĀĮŠĪŹĢā£ŗ
£Øµ„Ī»£ŗŠ”Ź±£©£¬²¢øł¾Żµ÷²é½į¹ūĮŠ³öĶ³¼Ę±ķ£¬»ęÖĘ³ÉÉČŠĪĶ³¼ĘĶ¼£¬ČēĶ¼ĖłŹ¾£®ĒėÄćøł¾ŻĶ¼±ķĢį¹©µÄŠÅĻ¢½ā“šĻĀĮŠĪŹĢā£ŗ
Ę½¾łĆæĢģĖÆĆߏ±¼ä·Ö×éĶ³¼Ę±ķ
×鱚ŠņŗÅ | ĖÆĆߏ±¼ä | ČĖŹż£ØʵŹż£© |
|
|
|
|
|
|
|
|
|
|
|
|
Ę½¾łĆæĢģĖÆĆߏ±¼äÉČŠĪĶ³¼Ę±ķ
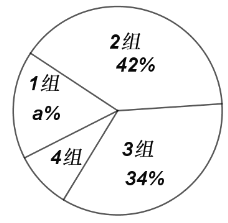
£Ø1£©![]() _______£¬
_______£¬![]() _______£¬
_______£¬![]() _______£Ø
_______£Ø![]() ĪŖ°Ł·ÖŗÅĒ°µÄŹż×Ö£©£»
ĪŖ°Ł·ÖŗÅĒ°µÄŹż×Ö£©£»
£Ø2£©Ė껜³éČ”µÄÕā²æ·ÖŃ§ÉśĘ½¾łĆæĢģĖÆĆߏ±¼äµÄÖŠĪ»ŹżĀäŌŚ_______×é£ØĢī×鱚ŠņŗÅ£©£»
£Ø3£©¹Ą¼ĘČ«Š£![]() Ćū¾ÅÄź¼¶Ń§ÉśÖŠĘ½¾łĆæĢģĖÆĆߏ±¼ä²»µĶÓŚ
Ćū¾ÅÄź¼¶Ń§ÉśÖŠĘ½¾łĆæĢģĖÆĆߏ±¼ä²»µĶÓŚ![]() Š”Ź±µÄѧɜӊ_______Ćū£»
Š”Ź±µÄѧɜӊ_______Ćū£»
£Ø4£©ČōĖł³é²éµÄĖÆĆߏ±¼ä![]() £ØŠ”Ź±£©µÄ
£ØŠ”Ź±£©µÄ![]() Ćūѧɜ£¬ĘäÖŠ
Ćūѧɜ£¬ĘäÖŠ![]() ĆūÄŠÉśŗĶ
ĆūÄŠÉśŗĶ![]() ĆūÅ®Éś£¬ĻÖ“ÓÕā
ĆūÅ®Éś£¬ĻÖ“ÓÕā![]() Ćūѧɜ֊Ė껜єȔ
Ćūѧɜ֊Ė껜єȔ![]() Ćūѧɜ²Ī¼Óøö±š·ĆĢø£¬ĒėÓĆĮŠ±ķ»ņ»Ź÷דĶ¼µÄ·½·ØĒóєȔµÄ
Ćūѧɜ²Ī¼Óøö±š·ĆĢø£¬ĒėÓĆĮŠ±ķ»ņ»Ź÷דĶ¼µÄ·½·ØĒóєȔµÄ![]() ĆūѧɜĒ”ĪŖ
ĆūѧɜĒ”ĪŖ![]() ÄŠ
ÄŠ![]() Å®µÄøÅĀŹ£®
Å®µÄøÅĀŹ£®