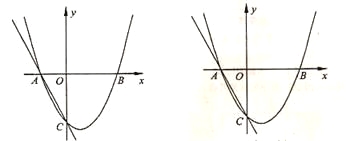��Ŀ����
����Ŀ����һԪ���η����У���������Τ�ﶨ��������һԪ���η���![]() ���������������ʵ����
���������������ʵ����![]() ����ô
����ô![]() ��˵������������������
��˵������������������![]() �������緽��
�������緽��![]() �У�
�У�![]() �����Ը÷������������ȵ�ʵ�������Ƿ��̵�����Ϊ
�����Ը÷������������ȵ�ʵ�������Ƿ��̵�����Ϊ![]() ��
��![]() ����ô
����ô![]() +
+![]() =
=![]() ��
��![]()
![]() =
=![]() ,������Ķ����Ͻ�����и��⣺
,������Ķ����Ͻ�����и��⣺
��1����֪����![]() ������Ϊ
������Ϊ![]() ��
��![]() ����
����![]() >
>![]() ,�����и�ʽ��ֵ:
,�����и�ʽ��ֵ:
��![]() ��
��![]()
��2����֪![]() ��һԪ���η���
��һԪ���η���![]() ������ʵ������
������ʵ������
���Ƿ����ʵ��![]() ��ʹ
��ʹ![]() �����������ڣ����
�����������ڣ����![]() ��ֵ���������ڣ���˵�����ɣ�
��ֵ���������ڣ���˵�����ɣ�
����ʹ![]() ��ֵΪ������ʵ��
��ֵΪ������ʵ��![]() ������ֵ��
������ֵ��
���𰸡���1����13��-![]() ��2���ٲ����ڢ�-2,-3��-5
��2���ٲ����ڢ�-2,-3��-5
��������
��1�����ݸ���ϵ���Ĺ�ϵ���![]() +
+![]() ��
��![]() ��ֵ���Ѣ��䷽���Ѣ�ͨ�֣�Ȼ���
��ֵ���Ѣ��䷽���Ѣ�ͨ�֣�Ȼ���![]() +
+![]() ��
��![]() ��ֵ������㼴�ɣ�
��ֵ������㼴�ɣ�
��2�����ݷ���������ʵ���������![]() +
+![]() ��
��![]() ��ֵ����
��ֵ����![]() ��ȡֵ��Χ���ٰ�����ʽ�ӻ������룬��
��ȡֵ��Χ���ٰ�����ʽ�ӻ������룬��![]() +
+![]() ��
��![]() ��ֵ���룬�������
��ֵ���룬�������![]() ��ֵ����ͨ�ֺ�
��ֵ����ͨ�ֺ�![]() +
+![]() ��
��![]() ��ֵ���룬���ۼ���.
��ֵ���룬���ۼ���.
��1���߷���![]() ������Ϊ
������Ϊ![]() ��
��![]() ����
����![]() >
>![]() ��
��
��![]() =3 ��
=3 �� ![]() =-2 ��
=-2 ��
��![]() =
=![]() =9+4=13��
=9+4=13��
![]() =
=![]() ��
��
��2����![]() ��һԪ���η���
��һԪ���η���![]() ������ʵ������
������ʵ������
��![]() �� ��k<0��
�� ��k<0��
![]() =1 ,
=1 , ![]() =
=![]() ��
��
�������������ʵ��k.��![]()
=![]() ��
��
��� ![]() ��
��
��k<0 �� �����������ʵ��k ��
��![]()
=![]()
=-![]() ��
��
Ҫʹ-![]() Ϊ���� �� ��
���� �� ��![]() ��
��
��k=0,-2,1,-3,-5,3 ��
�֡�k<0 �� ��k=-2,-3��-5.

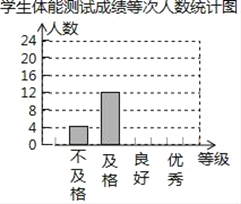
����Ŀ��ijУΪ�˽�ѧ������������Ӹ��꼶�����ȡ����ѧ���������ܲ��ԣ�ÿ��ѧ���IJ��Գɼ�������ӦΪ���㡢���á����������ĸ��ȼ���ͳ��Ա�ڽ��������ݻ��Ƴ�ͼ��ʱ���֣�����©ͳ��4�ˣ�����©ͳ��6�ˣ����Ǽ�ʱ�������Ӷ��γ���ͼͼ�����밴��ȷ���ݽ�����и��⣺
ѧ�����ܲ��Գɼ����ȴ�����ͳ�Ʊ�
���ܵȼ� | ����ǰ���� | ���������� |
���� | 8 | �� �� |
���� | 16 | �� �� |
���� | 12 | �� �� |
������ | 4 | �� �� |
�ϼ� | 40 | �� �� |
��1����дͳ�Ʊ���
��2�����ݵ��������ݣ���ȫ����ͳ��ͼ��
��3������У����ѧ��1500�ˣ�����������У���ܲ��Եȼ�Ϊ����������������