题目内容
直线AB，CD，EF相交于点O，且∠AOD=100°，∠1=30°，求∠2的度数．
解：根据对顶角相等，得∠DOF=∠1=30°．
又∵∠AOD+∠DOF+∠2=180°，∠AOD=100°，
∴∠2=180°-∠AOD-∠DOF
=180°-100°-30°=50°．
分析：由∠1与∠DOF是对顶角，而∠DOF，∠AOD，∠2三角的和是180°，因而就可以求出∠2的度数．
点评：熟练掌握对顶角的性质找出各角之间的关系是解决本题的关键．
又∵∠AOD+∠DOF+∠2=180°，∠AOD=100°，
∴∠2=180°-∠AOD-∠DOF
=180°-100°-30°=50°．
分析：由∠1与∠DOF是对顶角，而∠DOF，∠AOD，∠2三角的和是180°，因而就可以求出∠2的度数．
点评：熟练掌握对顶角的性质找出各角之间的关系是解决本题的关键．
练习册系列答案
学业测评一课一测系列答案
小学课时作业全通练案系列答案
相关题目
10、如图，直线AB，CD，EF相交于点O，则∠AOC的对顶角是∠
7、如图，已知直线AB、CD、EF相交于点O，∠1=95°，∠2=32°，则∠BOE=
12、如图，直线AB，CD，EF相交于点O，且AB⊥CD，∠1与∠2的关系是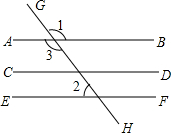
如图，直线AB、CD、EF被直线GH所截，已知AB∥CD，∠1+∠2=180°，请填写CD∥EF的理由．
如图所示，直线AB、CD、EF相交于点O，且EF⊥CD，若∠AOE=30°，则∠AOC=