Question

【题目】在平面直角坐标系中，如果某点的横坐标与纵坐标的和为10，则称此点为“合适点”例如，点（1，9），（﹣2019，2029）…都是“合适点”．

（1）求函数y＝2x+1的图象上的“合适点”的坐标；

（2）求二次函数y＝x2﹣5x﹣2的图象上的两个“合适点”A，B之间线段的长；

（3）若二次函数y＝ax2+4x+c的图象上有且只有一个合适点”，其坐标为（4，6），求二次函数y＝ax2+4x+c的表达式；

（4）我们将抛物线y＝2（x﹣n）2﹣3在x轴下方的图象记为G1，在x轴及x轴上方图象记为G2，现将G1沿x轴向上翻折得到G3，图象G2和图象G3两部分组成的记为G，当图象G上恰有两个“合适点”时，直接写出n的取值范围．

Answer 1

【答案】（1）（3，7）；（2）8；（3）y＝﹣x2+4x；（4）n＜或10﹣＜n＜10+

【解析】

（1）根据“合适点”的定义，联立x+y＝10和y＝2x+1即可求解；

（2）根据“合适点”的定义，联立x+y＝10和y＝x2﹣5x﹣2即可求解；

（3）将点（4，6）代入二次函数表达式得：16a+16+c＝6…①，联立y＝10﹣x和y＝ax2+4x+c并整理得：2x2+5x+（c﹣10）＝0，△＝25﹣4a（c﹣10）＝0…②，联立①②即可求解；

（4）当直线m于图象G3只有一个交点时，直线m与图象G有3个“合适点”；当直线m经过点A、B时，直线m与图象G有3个“合适点”，即可求解．

解：（1）联立

解得：

故“合适点”的坐标为（3，7）；

（2）联立

解得：或

故点A、B的坐标分别为：（﹣2，12）、（6，4），

则AB＝＝8；

（3）将点（4，6）代入二次函数表达式得：

16a+16+c＝6…①，

联立y＝10﹣x和y＝ax2+4x+c并整理得：

ax2+5x+（c﹣10）＝0，

由题意可知：△＝25﹣4a（c﹣10）＝0…②，

联立①②并解得：a＝﹣，c＝0，

故抛物线的表达式为：y＝﹣x2+4x；

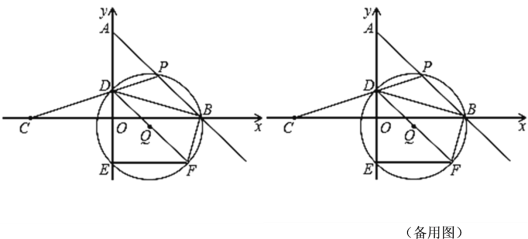
（4）图象G，如下图所示：

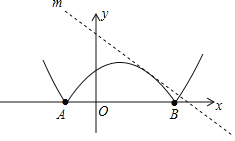
∵G1的顶点坐标为（n，-3），G1的函数表达式为：y＝2（x﹣n）2-3，

∴G3的顶点坐标为（n，3），则G3的函数表达式为：y＝﹣2（x﹣n）2+3，

x+y＝10，则y＝10﹣x，

设直线m为：y＝10﹣x，

①当直线m与图象G3只有一个交点时，由图可知：直线m与G2有两个交点

直线m与图象G有3个交点，即有3个“合适点”，

联立直线m与G3的表达式得：y＝﹣2（x﹣n）2+3＝10﹣x，整理得：

2x2﹣（4n+1）x+（2n2+7）＝0，

△＝b2﹣4ac＝8n﹣55＝0，解得：n＝，

故当n＜时，图象G恰好有2个“合适点”；

②当直线m经过点A、B时，

直线m与图象G有3个交点，即有3个“合适点”，则在这两个点之间有2个“合适点”，

直线m与x轴的交点为（10，0），

将（10，0）代入y＝2（x﹣n）2﹣3并解得：n＝10，

故10﹣＜n＜10+；

综上，n的取值范围为：n＜或10﹣＜n＜10+．