题目内容
8.一个矩形的两条对角线的一个夹角为60°,对角线长为10,则这个矩形的面积为( )| A. | 25 | B. | 50 | C. | 25$\sqrt{3}$ | D. | 50$\sqrt{3}$ |
分析 根据矩形的对角线互相平分且相等求出OA=OB=5,然后判断出△AOB是等边三角形,根据等边三角形的性质求出AB,再利用勾股定理列式求出BC,然后根据矩形的面积公式列式计算即可得解.
解答 解:如图,∵四边形ABCD是矩形,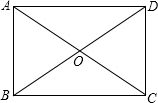
∴OA=OB=$\frac{1}{2}$×10=5,
∵∠AOB=60°,
∴△AOB是等边三角形,
∴AB=OA=5,
由勾股定理得,BC=$\sqrt{A{C}^{2}-A{B}^{2}}$=$\sqrt{1{0}^{2}-{5}^{2}}$=5$\sqrt{3}$,
∴矩形的面积=BC•AB=5$\sqrt{3}$×5=25$\sqrt{3}$.
故选C.
点评 本题考查了矩形的性质,等边三角形的判定与性质,勾股定理,熟记性质是解题的关键,作出图形更形象直观.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
16.下列美丽的车标中是轴对称图形的个数有( )


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
17.将正整数1,2,3,…从小到大按下面规律排列,则第i行第j列的数为n(i-1)+j(用i,j表示).
| 第1列 | 第2列 | 第3列 | … | 第n列 | |
| 第1行 | 1 | 2 | 3 | … | n |
| 第2行 | n+1 | n+2 | n+3 | … | 2n |
| 第3行 | 2n+1 | 2n+2 | 2n+3 | … | 3n |
| … | … | … | … | … | … |
18.在-2,$\frac{1}{2}$,0,-$\frac{2}{3}$,-0.7,π,15%中,分数有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
 如图,
如图,