题目内容
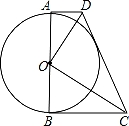
如图,已知☉O的直径AB=8,过A、B两点作☉O的切线AD、BC.
(1)当AD=2,BC=8时,连接OC、OD、CD.
①求△COD的面积.
②试判断直线CD与☉O的位置关系,并说明理由.
(2)若直线CD与☉O相切于点E,设AD=x(x>0),试用含x的式子表示四边形ABCD的面积S,并探索S是否存在最小值,写出探索过程.
【考点】圆的综合题.
【分析】(1)①利用已知结合梯形面积以及三角形面积求法得出答案;
②过点O作OF⊥CD于F,得出OF的长,再利用切线的判定方法得出答案;
(2)利用勾股定理得出y与x之间的关系,再利用一元二次方程根的判别式得出S的最值.
【解答】解:(1)①由题意可得:
∵S梯形ABCD=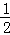 (AD+BC)•AB=40,S△AOD=
(AD+BC)•AB=40,S△AOD=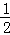 AD•AO=4,
AD•AO=4,
S△BOC=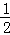 BC•BO=16,
BC•BO=16,
∴S△COD=40﹣4﹣16=20;
②直线CD与☉O相切,
理由如下:过点D作DE⊥BC于E,则四边形ABED是矩形
∴DE=AB=8,BE=AD=2
∴CE=6
在Rt△CDE中,CD= =10,
=10,
过点O作OF⊥CD于F,则S△COD=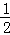 CD•OF=20,
CD•OF=20,
解得:OF=4,
即OF=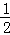 AB,
AB,
故直线CD与☉O相切;
(2)设BC=y,则CD=x+y,CE=|y﹣x|,
在Rt△DCE中,DC2﹣CE2=DE2,
即(x+y)2﹣(y﹣x)2=64,
则y= (x>0),
(x>0),
∴S=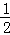 (AD+BC)•AB
(AD+BC)•AB
=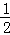 (x+
(x+ )×8
)×8
=4x+ (x>0),
(x>0),
故4x2﹣Sx+64=0(x>0),
∵该方程是关于x的一元二次方程,且此方程一定有解,
∴△=S2﹣1024≥0,
根据二次函数解得:S≥32或S≤﹣32(负值舍去),
∴S≥32,
∴S有最小值,最小值为32.

【点评】此题主要考查了圆的综合以及一元二次方程根的判别式和切线的判定、勾股定理等知识,正确掌握切线的判定方法作出辅助线是解题关键.


 )
) 的值.
的值. ),解答下列问题:
),解答下列问题: ,且地面总面积是卫生间面积的15倍,铺1
,且地面总面积是卫生间面积的15倍,铺1