题目内容
【题目】如图,△ABC为等腰直角三角形,∠B=90°,AB=2,把△ABC绕点A逆时针旋转60°得到△AB1C1,连接CB1,则点B1到直线AC的距离为_____.
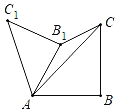
【答案】![]() .
.
【解析】
连接CC1,过点B1作B1H⊥AC,由旋转的性质可得AC=AC1=2![]() ,∠CAC1=60°,AB1=AB=2,BC=B1C1=2,可得∴△ACC1是等边三角形,由“SSS”可证△AB1C≌△C1B1C,可得S△AB1C=S△C1B1CS,由三角形的面积关系可求解.
,∠CAC1=60°,AB1=AB=2,BC=B1C1=2,可得∴△ACC1是等边三角形,由“SSS”可证△AB1C≌△C1B1C,可得S△AB1C=S△C1B1CS,由三角形的面积关系可求解.
如图,连接CC1,过点B1作B1H⊥AC,
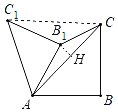
∵∠B=90°,AB=BC=2,
∴AC=2![]() ,
,
∵把△ABC绕点A逆时针旋转60°得到△AB1C1,
∴AC=AC1=2![]() ,∠CAC1=60°,AB1=AB=2,BC=B1C1=2,
,∠CAC1=60°,AB1=AB=2,BC=B1C1=2,
∴△ACC1是等边三角形,
∴C1C=AC,B1C=B1C,AB1=B1C1,
∴△AB1C≌△C1B1C(SSS)
![]()
![]()
∴![]() ×(2
×(2![]() )2=
)2=![]() ×2×2+2×
×2×2+2×![]() ×2
×2![]() ×B1H,
×B1H,
∴B1H=![]() ,
,
故答案为:![]() .
.

练习册系列答案
相关题目
【题目】小明对函数y=﹣|x2﹣4|的图象和性质进行了探究,其探究过程中的列表如下:
x | … | -3 | ﹣2 | -1 | 0 | 1 | 2 | 3 | … |
y | … | m | 0 | -3 | n | -3 | 0 | -5 | … |
(1)求表中m,n的值;
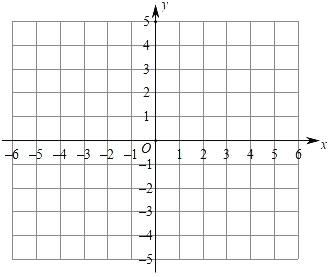
(2)根据表中数据,在如图所示的平面直角坐标系中描点,并画出了该函数的图象;
(3)观察函数图象,写出一条函数的性质;
(4)结合你所画的函数图象,直接写出不等式﹣|x2﹣4|>x﹣2的解集.