题目内容
18.已知点A(4,y1),B($\sqrt{2}$,y2),C(-2,y3)都在二次函数y=x2-4x+m的图象上,则y1,y2,y3的大小关系是y2<y1<y3.分析 根据函数解析式的特点,其对称轴为x=2,图象开口向上,y随x的增大而减小,据二次函数图象的对称性可知,A(4,y1)与(0,y1)关于对称轴对称,由$\sqrt{2}$>0>-2,可判断y2<y1<y3.
解答 解:∵二次函数y=x2-4x-m,
∴对称轴为x=2,
B($\sqrt{2}$,y2),C(-2,y3)在对称轴的左侧,y随x的增大而减小,
根据二次函数图象的对称性可知,A(4,y1)与(0,y1)关于对称轴对称,
因为$\sqrt{2}$>0>-2,故y2<y1<y3,
故答案为y2<y1<y3.
点评 题考查了函数图象上的点的坐标与函数解析式的关系,同时考查了函数的对称性及增减性.

练习册系列答案
相关题目
8. 如图所示的立体图形的主视图是( )
如图所示的立体图形的主视图是( )
 如图所示的立体图形的主视图是( )
如图所示的立体图形的主视图是( )| A. |  | B. |  | C. |  | D. |  |
9. 一个三棱柱如图所示,它的主视图是( )
一个三棱柱如图所示,它的主视图是( )
 一个三棱柱如图所示,它的主视图是( )
一个三棱柱如图所示,它的主视图是( )| A. |  | B. |  | C. |  | D. |  |
6.如图四个几何体,其中,它们各自的主视图与俯视图不相同的几何体的个数是( )


| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
7.某学校九年级8班10名学生积极奉献爱心,自发组织捐款,支援贫困山区儿童,若他们捐款的数额分别是(单位:元):10,15,20,10,5,15,10,5,10,5,则这组捐款的众数和中位数分别是( )
| A. | 5元、10元 | B. | 15元、5元 | C. | 10元、15元 | D. | 10元、10元 |
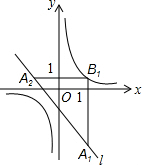 如图,在平面直角坐标系xOy中,已知直线l:y=-x-1,双曲线y=$\frac{1}{x}$,在l上取一点A1,过A1作x轴的垂线交双曲线于点B1,过B1作y轴的垂线交l于点A2,请继续操作并探究:过A2作x轴的垂线交双曲线于点B2,过B2作y轴的垂线交l于点A3,…,这样依次得到l上的点A1,A2,A3,…,An,…记点An的横坐标为an,若a1=2,则a2=-$\frac{3}{2}$,a2016=-$\frac{1}{3}$;若要将上述操作无限次地进行下去,则a1不可能取的值是0或-1.
如图,在平面直角坐标系xOy中,已知直线l:y=-x-1,双曲线y=$\frac{1}{x}$,在l上取一点A1,过A1作x轴的垂线交双曲线于点B1,过B1作y轴的垂线交l于点A2,请继续操作并探究:过A2作x轴的垂线交双曲线于点B2,过B2作y轴的垂线交l于点A3,…,这样依次得到l上的点A1,A2,A3,…,An,…记点An的横坐标为an,若a1=2,则a2=-$\frac{3}{2}$,a2016=-$\frac{1}{3}$;若要将上述操作无限次地进行下去,则a1不可能取的值是0或-1.